题目内容
探索性问题
数轴上两点间的距离，如2与3的距离可表示为|2-3|=1，2与-3的距离可表示为|2-（-3）|=5
（1）若A、B两点表示的数为a，b．且A、B两点间的距离记为d，试问d和a、b有何数量关系？
（2）在数轴上标出所有符合条件的整数点P，使它到5和-5的距离之和为10，并求所有这些整数的和．
（3）若点C表示的数为x，当点C在什么位置时，|x+1|+|x-2|取得的值最小？
数轴上两点间的距离，如2与3的距离可表示为|2-3|=1，2与-3的距离可表示为|2-（-3）|=5
（1）若A、B两点表示的数为a，b．且A、B两点间的距离记为d，试问d和a、b有何数量关系？
（2）在数轴上标出所有符合条件的整数点P，使它到5和-5的距离之和为10，并求所有这些整数的和．
（3）若点C表示的数为x，当点C在什么位置时，|x+1|+|x-2|取得的值最小？
分析：（1）根据数轴的知识，结合所给例题即可得出答案．
（2）由数轴的知识，可得出只要在-5和5之间的整数均满足题意．
（3）根据绝对值的几何意义，可得出-1和2之间的任何一点均满足题意．
（2）由数轴的知识，可得出只要在-5和5之间的整数均满足题意．
（3）根据绝对值的几何意义，可得出-1和2之间的任何一点均满足题意．
解答：解：（1）|a-b|=d；
（2）如图所示：
，
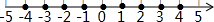4+3+2+1+0+（-1）+（-2）+（-3）+（-4）=0；
（3）根据数轴的几何意义可得-1和2之间的任何一点均能使|x+1|+|x-2|取得的值最小．
故可得：点C的范围在：-1≤x≤2时，能满足题意．
（2）如图所示：
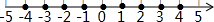，4+3+2+1+0+（-1）+（-2）+（-3）+（-4）=0；
（3）根据数轴的几何意义可得-1和2之间的任何一点均能使|x+1|+|x-2|取得的值最小．
故可得：点C的范围在：-1≤x≤2时，能满足题意．
点评：此题考查了绝对值函数的最值、数轴及两点间的距离，解答本题的关键是理解绝对值的几何意义，可以借助坐标轴演示．
练习册系列答案
阅读快车系列答案
相关题目
探索性问题：探索性问题
数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形
结合”的基础。请利用数轴回答下列问题：
已知点A、B在数轴上分别
表示数a、b.
(1)填写下表：
| 数 | 列A | 列B | 列C | 列D | 列E | 列F |
| a | 5 | -5 | -6 | -6 | -10 | -2.5 |
| b | 3 | 0 | 4 | -4 | 2 | -2.5 |
| A、B两点的距离 |
(2)任取上表一列数，你发现距离表示可列式为 ，则轴上表示
和
的两点之间的距离可表示为 .
(3)若表示一个有理数，且
，则
= .
(4)若A、B两点的距离为 d，则d与a、b有何数量关系.