题目内容
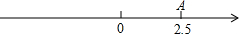 探索性问题:
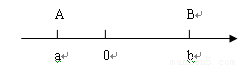
探索性问题:(1)如图,先在数轴上画出表示2.5的相反数的点B,再把点A向左移动1.5个单位,得到点C,求点B,C表示的数分别为
-2.5、1
-2.5、1
,B,C两点间的距离是3.5
3.5
.(2)数轴上表示x和-1的两点A和B之间的距离表示为
|x+1|
|x+1|
,如果|AB|=3,那么x为2或-4
2或-4
;(3)若点A表示的整数为x,则当x为
-1
-1
时,|x+4|与|x-2|的值相等.(4)要使代数式|x+5|+|x-2|取最小值时,相应的x的取值范围是
-5≤x≤2
-5≤x≤2
.分析:(1)在数轴上找到点B,及点C的位置,结合数轴可得出B、C表示的数,B、C两点间的距离;
(2)根据数轴上的点的坐标,即可求出A和B之间的距离;然后建立方程可解出x的值.
(3)若|x+4|与|x-2|的值相等表示一个点到点-4和到点2的距离相等,结合数轴可得出答案.
(4)由以上的解答可得,只要满足在-5与点2之间的点即能使代数式|x+5|+|x-2|取最小值.
(2)根据数轴上的点的坐标,即可求出A和B之间的距离;然后建立方程可解出x的值.
(3)若|x+4|与|x-2|的值相等表示一个点到点-4和到点2的距离相等,结合数轴可得出答案.
(4)由以上的解答可得,只要满足在-5与点2之间的点即能使代数式|x+5|+|x-2|取最小值.
解答:解:(1)各点的位置如图所示:

∴点B,C表示的数分别为-2.5、1;B、C两点间的距离是3.5;
(2)表示x和-1的两点A和B之间的距离表示为|x+1|,
若|AB|=3,即|x+1|=3,
解得:x=2或-4;
(3)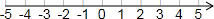
结合数轴可得若点A表示的整数为x,则当x=-1时,|x+4|与|x-2|的值相等.
(4)只要满足在-5与点2之间的点即能使代数式|x+5|+|x-2|取最小值,
故x的取值范围为:-5≤x≤2.
故答案为:-2.5、1,3.5;|x+1|、2或-4;-1;-5≤x≤2.

∴点B,C表示的数分别为-2.5、1;B、C两点间的距离是3.5;
(2)表示x和-1的两点A和B之间的距离表示为|x+1|,
若|AB|=3,即|x+1|=3,
解得:x=2或-4;
(3)
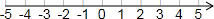
结合数轴可得若点A表示的整数为x,则当x=-1时,|x+4|与|x-2|的值相等.
(4)只要满足在-5与点2之间的点即能使代数式|x+5|+|x-2|取最小值,
故x的取值范围为:-5≤x≤2.
故答案为:-2.5、1,3.5;|x+1|、2或-4;-1;-5≤x≤2.
点评:此题考查了绝对值函数的最值问题,解答本题的关键是掌握绝对值的几何意义,一定要结合数轴进行解答,不要凭空想象,有一定难度.

练习册系列答案
相关题目


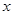 和
和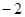 的两点之间的距离表示为 .
的两点之间的距离表示为 . ,则
,则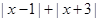 = .
= .

 和
和 的两点之间的距离表示为
.
的两点之间的距离表示为
.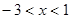 ,则
,则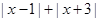 =
.
=
.