题目内容
在四边形ABCD中,AB、BC、CD、DA的中点分别为P、Q、M、N:

(1)如图1,试判断四边形PQMN为怎样的四边形,并证明你的结论;
(2)若在AB上取一点E,连结DE,CE,恰好△ADE和△BCE都是等边三角形(如图2):
①判断此时四边形PQMN的形状为
②当AE=6,EB=3,求此时四边形PQMN的周长(结果保留根号)

(1)如图1,试判断四边形PQMN为怎样的四边形,并证明你的结论;
(2)若在AB上取一点E,连结DE,CE,恰好△ADE和△BCE都是等边三角形(如图2):
①判断此时四边形PQMN的形状为
菱形
菱形
(直接写出你的结论)②当AE=6,EB=3,求此时四边形PQMN的周长(结果保留根号)
分析:(1)连结AC、BD.利用三角形中位线定理判定四边形PQMN的对边平行且相等,易证该四边形是平行四边形;
(2)①四边形PQMN是菱形;
②如图2,过点D作DF⊥AB于F,则通过解三角形求得DF=3
,由勾股定理得到DB=
=3
.由①知四边形PQMN是菱形,可计算得周长是6
.
(2)①四边形PQMN是菱形;
②如图2,过点D作DF⊥AB于F,则通过解三角形求得DF=3
| 3 |
(3
|
| 7 |
| 7 |
解答: 解:(1)连结AC、BD.∵PQ为△ABC的中位线,∴PQ
解:(1)连结AC、BD.∵PQ为△ABC的中位线,∴PQ
AC
同理 MN
AC.∴MN
PQ,∴四边形PQMN为平行四边形;
(2)①四边形PQMN是菱形;
②过点D作DF⊥AB于F,则DF=3
又DF2+FB2=DB2
∴DB=
=3
∴由①知四边形PQMN是菱形,可计算得周长是6
.
 解:(1)连结AC、BD.∵PQ为△ABC的中位线,∴PQ
解:(1)连结AC、BD.∵PQ为△ABC的中位线,∴PQ| ∥ |
. |
| 1 |
| 2 |
同理 MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
(2)①四边形PQMN是菱形;
②过点D作DF⊥AB于F,则DF=3
| 3 |
又DF2+FB2=DB2
∴DB=
(3
|
| 7 |
∴由①知四边形PQMN是菱形,可计算得周长是6
| 7 |
点评:本题考查了中点四边形.解题时,利用了三角形中位线的性质定理.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
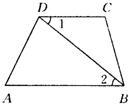 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
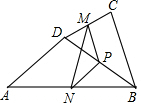 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?