题目内容
【题目】设二次函数![]() (
(![]() 为正常数)的图象与
为正常数)的图象与![]() 轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与![]() 轴交于C点.直线
轴交于C点.直线![]() 过M(0,m)(
过M(0,m)(![]() 且
且![]() )且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数
)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数![]() 的图象关于直线
的图象关于直线![]() 的对称图象与y轴交于点P.设直线PD与
的对称图象与y轴交于点P.设直线PD与![]() 轴交点为Q ,则:
轴交点为Q ,则:
⑴ 求A、C两点的坐标;
⑵ 求![]() 的值(用含m的代数式表示);
的值(用含m的代数式表示);
⑶ 是否存在实数m,使![]() ?若能,则求出相应的m的值;若不能,请说明理由.
?若能,则求出相应的m的值;若不能,请说明理由.
【答案】⑴ 点C的坐标为(0,2).点A坐标为(-1,0).
⑵ AD=![]() .
.
⑶当![]() >1时,才存在实数m使得
>1时,才存在实数m使得![]() ∽
∽![]() ,从而有
,从而有![]() ,此时
,此时![]() ;当0<
;当0<![]() 1时,不存在实数m使得
1时,不存在实数m使得![]() .
.
【解析】试题分析:(1)令y=0,可得A点的坐标,令x=0,可得C点的坐标;(2)根据A、C两个点的坐标求出直线AC的解析式,再求出点D的坐标,然后求出对应线段的长度,最后利用勾股定理即可求出AD;(3)要使CD·AQ=PQ·DE,因为∠PQA=∠PDE=∠CDE,所以只须△PQA∽△CDE,即须△PQA∽△PDE,分0 <m<1,1<m<2两个情况讨论求解即可.
试题解析:
⑴ 令y=0,可得:0=-![]() (x+1)(x-a),
(x+1)(x-a),
解得x1=-1,x2=a,
∵A在B的左侧,a>0,
∴A(-1,0),
令x=0,可得:y=-![]() ×(-a)=2,
×(-a)=2,
∴C(0,2).
故点C的坐标为(0,2),点A坐标为(-1,0).
(2)
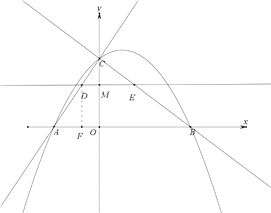
作DF⊥AB于点F,
∵A(-1,0),C(0,2),
∴直线AC解析式为:y=2x+2,
令y=m,m=2x+2,x=![]() -1,
-1,
∴D(![]() -1,m),
-1,m),
∴FO=1-![]() ,
,
∴AF=![]() ,
,
∵DF=m,
∴AD=![]() m.
m.
⑶连接AP、PE,
要使CD·AQ=PQ·DE,∵∠PQA=∠PDE=∠CDE,
∴只须△PQA∽△CDE,即须△PQA∽△PDE.

当0 <m<1时,点P在x轴下方,此时∠PQA显然为钝角,
而∠PDE显然为锐角,故此时不能有△PQA∽△CDE.
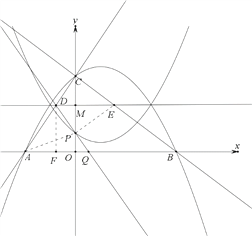
当1<m<2时,△PQA∽△PDE时,A、P、E三点共线,
∴△APO∽△EPM,
∴![]() =
=![]() ,
,
∵B(a,0),C(0,2),
∴直线BC解析式为:y=-![]() x+2,
x+2,
令![]() =
=![]() ,
,![]() =-
=-![]() +2,
+2,![]() =a-
=a-![]() ,
,
∴E(a-![]() ,m),
,m),
∴ME= a-![]() ,
,
∵CO=2,MO=m,
∴PM=CM=2-m,
∴PO=2m-2,
∴![]() =
=![]() ,
,
∴ ![]() ,而此时1<m<2,
,而此时1<m<2,
∴![]() ,
,
∴a>1.
综上所述,当a>1时,才存在实数m使得△PQA∽△CDE,从而有CD·AQ=PQ·DE,此时![]() ;当0<a≤1时,不存在实数
;当0<a≤1时,不存在实数![]() 使得CD·AQ=PQ·DE.
使得CD·AQ=PQ·DE.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某数学课外活动小组在做气体压强实验时,获得压强p(Pa)与体积V(cm3)之间有下列对应数据:
p(Pa) | … | 1 | 2 | 3 | 4 | 5 | … |
V(cm3) | … | 6 | 3 | 2 | 1.5 | 1.2 | … |
根据表中提供的信息,回答下列问题:
(1)猜想p与V之间的关系,并求出函数关系式;
(2)当气体的体积是12cm3时,压强是多少?



