题目内容
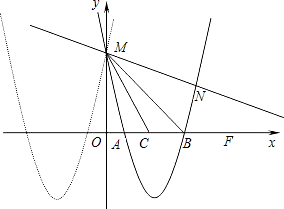 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.(1)求出y=mx2+nx+p的解析式,试猜想出与一般形式抛物线y=ax2+bx+c关于y轴对称的二次函数解析式(不要求证明);
(2)若A,B的中点是点C,求sin∠CMB;
(3)如果过点M的一条直线与y=mx2+nx+p图象相交于另一点N(a,b),a≠b且满足a2-a+q=0,b2-b+q=0(q为常数),求点N的坐标.
分析:(1)可先求出抛物线y=x2+6x+5的顶点坐标,然后根据两抛物线关于y轴对称得出所求抛物线的顶点,可用顶点式二次函数通式来设所求的抛物线的解析式,然后将两函数与y轴的交点M的坐标代入所求的抛物线中即可得出其解析式.
两抛物线关于y轴对称,其开口方向,开口大小以及与y轴的交点都一样,因此a、c的值不变,而两函数的对称轴关于y轴对称,因此b值互为相反数,因此与一般形式抛物线y=ax2+bx+c关于y轴对称的二次函数解析式为y=ax2-bx+c.
(2)本题要先求出A、B、M的坐标,过C作CD⊥BM于D,那么关键是求出CD和MC的长,可在直角三角形CDB中,用BC的长和∠MBA的正弦值求出CD的长,然后在直角三角形OCM中,根据勾股定理求出CM的长,据此可得出sin∠CMB的值.
(3)可设直线的解析式为y=kx+5;由于N是两函数的交点,因此可联立两函数的解析式,用k表示出a,b的值,由题意可知a,b为方程x2-x+q=0的两根,根据韦达定理可知a+b=1,由此可求出k的值,然后将k的值代入表示a,b的式子中即可求出N点的坐标.
两抛物线关于y轴对称,其开口方向,开口大小以及与y轴的交点都一样,因此a、c的值不变,而两函数的对称轴关于y轴对称,因此b值互为相反数,因此与一般形式抛物线y=ax2+bx+c关于y轴对称的二次函数解析式为y=ax2-bx+c.
(2)本题要先求出A、B、M的坐标,过C作CD⊥BM于D,那么关键是求出CD和MC的长,可在直角三角形CDB中,用BC的长和∠MBA的正弦值求出CD的长,然后在直角三角形OCM中,根据勾股定理求出CM的长,据此可得出sin∠CMB的值.
(3)可设直线的解析式为y=kx+5;由于N是两函数的交点,因此可联立两函数的解析式,用k表示出a,b的值,由题意可知a,b为方程x2-x+q=0的两根,根据韦达定理可知a+b=1,由此可求出k的值,然后将k的值代入表示a,b的式子中即可求出N点的坐标.
解答: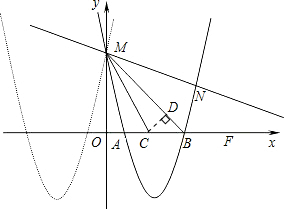 解:(1)y=x2+6x+5的顶点为(-3,-4),
解:(1)y=x2+6x+5的顶点为(-3,-4),
即y=mx2+nx+p的顶点的为(3,-4),
设y=mx2+nx+p=a(x-3)2-4,
y=x2+6x+5与y轴的交点M(0,5),
即y=mx2+nx+p与y轴的交点M(0,5).
即a=1,
所求二次函数为y=x2-6x+5.
猜想:与一般形式抛物线y=ax2+bx+c关于y轴对称的二次函数解析式是y=ax2-bx+c.
(2)过点C作CD⊥BM于D.
抛物线y=x2-6x+5与x轴的交点A(1,0),B(5,0),与y轴交点
M(0,5),AB中点C(3,0).
故△MOB,△BCD是等腰直角三角形,CD=
BC=2.
在Rt△MOC中,MC=
.
则sin∠CMB=
=
.
(3)设过点M(0,5)的直线为y=kx+5
,
解得
则a=k+6,b=k2+6k+5.
由已知a,b是方程x2-x+q=0的两个根,
故a+b=1.
即k+6+k2+6k+5=1,化简k2+7k+10=0,
则k1=-2,k2=-5.
点N的坐标是(4,-3)或(1,0).
 解:(1)y=x2+6x+5的顶点为(-3,-4),
解:(1)y=x2+6x+5的顶点为(-3,-4),即y=mx2+nx+p的顶点的为(3,-4),
设y=mx2+nx+p=a(x-3)2-4,
y=x2+6x+5与y轴的交点M(0,5),
即y=mx2+nx+p与y轴的交点M(0,5).
即a=1,
所求二次函数为y=x2-6x+5.
猜想:与一般形式抛物线y=ax2+bx+c关于y轴对称的二次函数解析式是y=ax2-bx+c.
(2)过点C作CD⊥BM于D.
抛物线y=x2-6x+5与x轴的交点A(1,0),B(5,0),与y轴交点
M(0,5),AB中点C(3,0).
故△MOB,△BCD是等腰直角三角形,CD=
| ||
| 2 |
在Rt△MOC中,MC=
| 34 |
则sin∠CMB=
| CD |
| MC |
| ||
| 17 |
(3)设过点M(0,5)的直线为y=kx+5
|
解得
|
|
则a=k+6,b=k2+6k+5.
由已知a,b是方程x2-x+q=0的两个根,
故a+b=1.
即k+6+k2+6k+5=1,化简k2+7k+10=0,
则k1=-2,k2=-5.
点N的坐标是(4,-3)或(1,0).
点评:考查一元二次方程根与系数的关系、二次函数解析式的确定、轴对称图形、函数图象交点等知识及综合应用知识、解决问题的能力.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;