题目内容
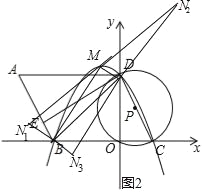
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
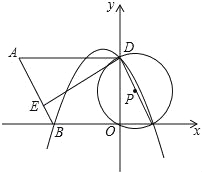
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() ;(2)证明见解析(3)点N的坐标为(﹣5,
;(2)证明见解析(3)点N的坐标为(﹣5,![]() )、(3,
)、(3,![]() )、(﹣3,﹣
)、(﹣3,﹣![]() )
)
【解析】
试题分析:(1)根据题意求得B的坐标,解直角三角形求得D的坐标,然后根据待定系数法即可求得;
(2)根据平行四边形的性质和直角三角形的性质求得AB=4,根据AE=3EB求得AE=3,易证得△AED∽△COD,得出∠ADE=∠CDO,由∠ADE+∠ODE=90°得出∠CDO+∠ODE=90,即可证得结论;
(3)把抛物线解析式化成顶点式,求得顶点M的坐标,然后结合B、D的坐标即可求得.
试题解析:(1)∵C(2,0),BC=6,
∴B(﹣4,0),
在Rt△OCD中,∵tan∠OCD=![]() ,
,
∴OD=2tan60°=2![]() ,
,
∴D(0,2![]() ),
),
设抛物线的解析式为y=a(x+4)(x﹣2),
把D(0,2![]() )代入得a4(﹣2)=2
)代入得a4(﹣2)=2![]() ,解得a=﹣
,解得a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x+4)(x﹣2)=﹣
(x+4)(x﹣2)=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() ;
;
(2)在Rt△OCD中,CD=2OC=4,
∵四边形ABCD为平行四边形,
∴AB=CD=4,AB∥CD,∠A=∠BCD=60°,AD=BC=6,
∵AE=3BE,
∴AE=3,
∴![]() ,
,
∵sin∠BCD=![]() ,
,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴∠DAE=∠DCB=60°,
∴△AED∽△COD,
∴∠ADE=∠CDO,
而∠ADE+∠ODE=90°
∴∠CDO+∠ODE=90°,
∴CD⊥DE,
∵∠DOC=90°,
∴CD为⊙P的直径,
∴ED是⊙P的切线;
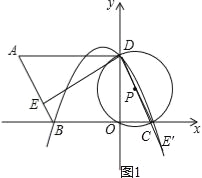
(3)存在.
∵y=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() =﹣
=﹣![]() (x+1)2+
(x+1)2+![]()
∴M(﹣1,![]() ),
),
而B(﹣4,0),D(0,2![]() ),如图2,
),如图2,
当BM为平行四边形BDMN的对角线时,点D向左平移4个单位,再向下平移2![]() 个单位得到点B,
个单位得到点B,
则点M(﹣1,![]() )向左平移4个单位,再向下平移2
)向左平移4个单位,再向下平移2![]() 个单位得到点N1(﹣5,
个单位得到点N1(﹣5,![]() );
);
当DM为平行四边形BDMN的对角线时,点B向右平移3个单位,
再向上平移![]() 个单位得到点M,则点D(0,2
个单位得到点M,则点D(0,2![]() )向右平移3个单位,再向上平移
)向右平移3个单位,再向上平移![]() 个单位得到点N2(3,
个单位得到点N2(3,![]() );
);
当BD为平行四边形BDMN的对角线时,点M向左平移3个单位,
再向下平移![]() 个单位得到点B,则点D(0,2
个单位得到点B,则点D(0,2![]() )向右平移3个单位,再向下平移
)向右平移3个单位,再向下平移![]() 个单位得到点N3(﹣3,﹣
个单位得到点N3(﹣3,﹣![]() ).
).
综上所述,点N的坐标为(﹣5,![]() )、(3,
)、(3,![]() )、(﹣3,﹣
)、(﹣3,﹣![]() ).
).