Question

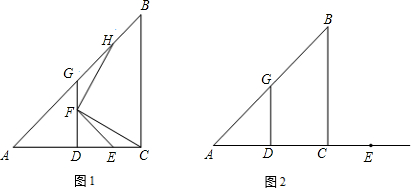
在Rt△ABC中，AC=BC，∠ACB=90°，D是AC的中点，DG⊥AC交AB于点G．
（1）如图1，E为线段DC上任意一点，点F在线段DG上，且DE=DF，连接EF与 CF，过点F作FH⊥FC，交直线AB于点H．
①求证：DG=DC；
②判断FH与FC的数量关系并加以证明．
（2）若E为线段DC的延长线上任意一点，点F在射线DG上，（1）中的其他条件不变，借助图2画出图形．在你所画图形中找出一对全等三角形，并判断你在（1）中得出的结论是否发生改变，（本小题直接写出结论，不必证明）．

Answer 1

分析：（1）①根据已知首先得出∠ADG=90°，进而求出AD=DG，得出DG=DC；
②利用已知首先得出∠GFH=∠ECF与∠HGF=∠FEC，再利用GF=EC得出△FGH≌△CEF，进而得出FH=FC；
（2）根据题意画出图形，再利用②中方法即可得出FH=FC．

解答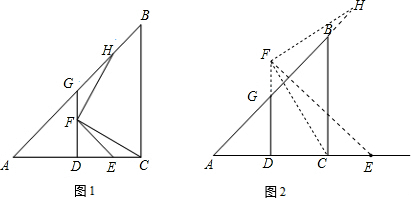：解：（1）①证明：∵AC=BC，∠ACB=90°，
∴∠A=∠B=45°，
又GD⊥AC，
∴∠ADG=90°，
在△ADG中，
∠A+∠ADG+∠AGD=180°，
∴∠AGD=45°，
∴∠A=∠AGD，
∴AD=DG，
又D是AC中点，
∴AD=CD，
∴DG=DC，
②由①DG=DC，
又∵DF=DE，
∴DG-DF=DC-DE，
即FG=CE，
由①∠AGD=45°，
∴∠HGF=180°-45°=135°，
又DE=DF，∠EDF=90°，
∴∠DEF=45°，
∴∠CEF=180°-45°=135°，
∴∠HGF=∠FEC，
又HF⊥CF，
∴∠HFC=90°，
∴∠GFH+∠DFC=180°-90°=90°，
又Rt△FDC中，
∠DFC+∠ECF=90°，
∴∠GFH=∠ECF，
在△FGH和△CEF中

∠HGF=∠FEC GF=EC ∠GFH=∠ECF

，
∴△FGH≌△CEF（ASA），
∴FH=FC；

（2）如图所示，
△FHG≌△CFE，
不变，FH=FC．

点评：此题主要考查了全等三角形的证明以及利用已知画出图形，熟练掌握全等三角形的判定以及利用已知条件画出几何图形是考查重点．