题目内容
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为对角线
为对角线![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,过
,过![]() 点作
点作![]() ,交直线
,交直线![]() 于点
于点![]() .
.![]() 点从
点从![]() 点出发,沿着
点出发,沿着![]() 方向以每秒
方向以每秒![]() 的速度运动,当点
的速度运动,当点![]() 与点
与点![]() 重合时,运动停止.设
重合时,运动停止.设![]() 的面积为
的面积为![]() ,
,![]() 点的运动时间为
点的运动时间为![]() 秒.
秒.
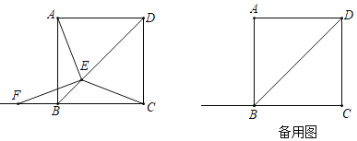
(1)求证:![]() ;
;
(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;
(3)求![]() 面积的最大值.
面积的最大值.
【答案】(1)证明见解析;(2) 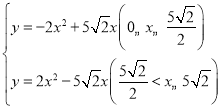 ;(3)
;(3)![]() 面积的最大值是50.
面积的最大值是50.
【解析】
(1)作辅助线,构建三角形全等,证明△AEM≌△EFN和△ADE≌△CDE(SAS),可得AE=CE=EF;
(2)分两种情况:根据三角形的面积公式可得y与x之间关系的函数表达式,根据勾股定理计算BD的长可得x的取值;
(3)根据(2)中的两种情况,分别利用配方法和二次函数的增减性可得结论.
(1)证明:过![]() 作
作![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,
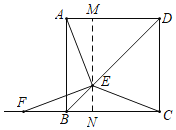
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:在Rt△BCD中,由勾股定理得:![]() ,
,
∴0≤x≤5![]() ,
,
由题意得:BE=2x,
∴BN=EN=![]() x,
x,
由(1)知:AE=EF=EC,
分两种情况:
①当0≤x≤![]() 时,如图1,
时,如图1,
∵AB=MN=10,
∴ME=FN=10-![]() x,
x,
∴BF=FN-BN=10-![]() x-
x-![]() x=10-2
x=10-2![]() x,
x,
∴y![]() ;
;
②当![]() <x≤5
<x≤5![]() 时,如图2,过E作EN⊥BC于N,
时,如图2,过E作EN⊥BC于N,
∴EN=BN=![]() x,
x,
∴FN=CN=10-![]() x,
x,
∴BF=BC-2CN=10-2(10-![]() x)=2
x)=2![]() x-10,
x-10,
∴y=![]() ;
;
综上,y与x之间关系的函数表达式为: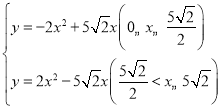 ;
;
(3)解:①当0≤x≤![]() 时,如图1,
时,如图1,
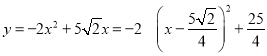 ,
,
∵-2<0,
∴当x=![]() 时,y有最大值是
时,y有最大值是![]() ;
;
②当![]() <x≤5
<x≤5![]() 时,如图2,
时,如图2,
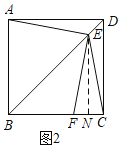
∴y=2x2-5![]() x=2(x-
x=2(x-![]() )2-
)2-![]() ,
,
∵2>0,
∴当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
∴当x=5![]() 时,y有最大值是50;
时,y有最大值是50;
综上,△BEF面积的最大值是50.

练习册系列答案
相关题目