题目内容
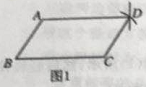
【题目】盈盈同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证
已知:如图1,在四边形ABCD中,BC=AD,________________________
求证:________________________
(1)填空,补全已知和求证
(2)按盈盈的想法写出证明
(3)用文字叙述所证命题的逆命题为________________________

【答案】 AB=CD 四边形ABCD是平行四边形 平行四边形两组对边分别相等
【解析】分析:(1)根据题意,要利用两组对边相等证明平行四边形,先找出题目命题中的已知为两组对边分别相等,即可求解,从命题“两组对边分别相等的四边形是平行四边形”中可知结论是四边形是平行四边形,根据图形和命题中的结论即可求解,
(2)连接一组对角线,可利用”边边边”定理证明两三角形全等,根据全等三角形的性质可得对应角相等,再根据内错角相等两直线平行判定两组线段平行,最后根据平行四边形的定义即可证明四边形是平行四边形.
(3)根据逆命题的条件为原命题的结论,逆命题的结论为原命题的条件即可求解.
详解:(1)AB=CD,四边形ABCD是平行四边形,
(2)证明:连接BD,
在△ABD和△CDB中,
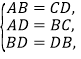 ,
,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠DBC,∠ABD=∠CDB,
∴AB∥CD,AD∥CB,
∴四边形ABCD是平行四边形,
(3)平行四边形两组对边分别相等.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目