题目内容
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a,以OC为一边作等边△OCD,连接AD.
(1)求证:△BOC≌△ADC;
(2)当OA=OD时,求a的值
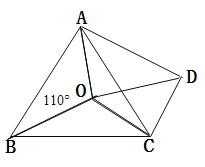
【答案】(1)证明见解析;(2)110°.
【解析】试题分析:(1)要证明△BOC≌△ADC,已知条件有AC=BC,CO=CD,
试题解析:
(1)∵△ABC是等边三角形,△COD是等边三角形,
∴BC=AC,CO=CD,∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC和△ADC中,
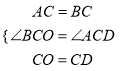 ,
,
∴△BOC≌△ADC;
(2)当OA=OD时,∠OAD=∠ODA,
∠OAD=∠DAC+∠OAC=∠OBC+∠OAC=360°-∠AOC-∠BOC-∠ACO-∠BCO=110°-60°=50°,
∴∠ODA=50°,
∴∠BOC=∠ADC=50°+60°=110°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




