题目内容
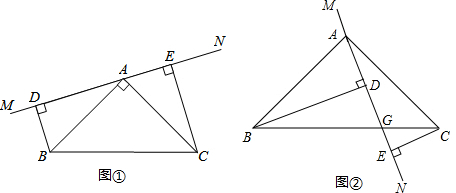
如图①所示,已知△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为点D、E.
(1)求证:DE=DB+EC
(2)如图②,将MN绕点A旋转,使MN和BC交于G点,其他条件不变,结论(1)还成立吗?若成立请给出证明;若不成立,请探究CE、DB、DE的关系,并证明你的结论.
(1)证明:∵由题意可知,BD⊥MN与D,EC⊥MN与E,∠BAC=90°,
∴∠BDA=∠CEA=∠BAC=90°,
∴∠DAB+∠EAC=90°,∠ECA+∠EAC=90°,
∴∠DAB=∠ECA,
在△ABD与△CEA中,
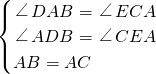
∴△ABD≌△CEA,
∴BD=AE,DA=CE,
∵DE=DA+AE,
∴DE=DB+EC.
(2)(1)的结论不成立,CE、DB、DE的关系是:BD=CE+DE,
证明:证明:∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
又∵BD⊥MN,CE⊥MN,
∴∠CAD+∠ACE=90°,∠BDA=∠AEC=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中

∴△ABD≌△CAE(AAS);
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
分析:(1)求出△ABD≌△CEA,根据全等三角形性质得出BD=AE,DA=CE,即可得出答案.
(2)求出△ABD≌△CAE,推出BD=AE,CE=AD,即可求出答案.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等,证明过程类似.
∴∠BDA=∠CEA=∠BAC=90°,
∴∠DAB+∠EAC=90°,∠ECA+∠EAC=90°,
∴∠DAB=∠ECA,
在△ABD与△CEA中,
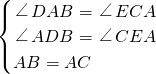
∴△ABD≌△CEA,
∴BD=AE,DA=CE,
∵DE=DA+AE,
∴DE=DB+EC.
(2)(1)的结论不成立,CE、DB、DE的关系是:BD=CE+DE,
证明:证明:∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
又∵BD⊥MN,CE⊥MN,
∴∠CAD+∠ACE=90°,∠BDA=∠AEC=90°,
∴∠BAD=∠ACE,
在△ABD和△CAE中

∴△ABD≌△CAE(AAS);
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
分析:(1)求出△ABD≌△CEA,根据全等三角形性质得出BD=AE,DA=CE,即可得出答案.
(2)求出△ABD≌△CAE,推出BD=AE,CE=AD,即可求出答案.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等,证明过程类似.

练习册系列答案
相关题目
 20、如图9所示,已知:∠α、线段a,求作等腰三角形△ABC,使腰长AB=a,底角∠A=∠α.(要求写出作法,并保留作图痕迹)
20、如图9所示,已知:∠α、线段a,求作等腰三角形△ABC,使腰长AB=a,底角∠A=∠α.(要求写出作法,并保留作图痕迹) (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
 所示.已知展开图中每个正方形的边长为1.
所示.已知展开图中每个正方形的边长为1.