题目内容

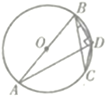
【题目】如图，AB是⊙O的直径，点C、D在⊙O上，连接AD、BC、BD、DC，若BD = CD，∠DBC = 20°，则，∠ABC =_________

【答案】50°

【解析】

先由直径所对的圆周角为90°，可得：∠ADB＝90°，由BD＝CD，∠DBC＝20°，根据等腰三角形性质可得：∠C＝20°，根据同弧所对的圆周角相等，即可求出∠A＝20°，根据三角形内角和定理求得∠ABD＝70°，进而即可求得∠ABC的度数．

∵AB是⊙O的直径，

∴∠ADB＝90°，

∵BD＝CD，∠DBC＝20°，

∴∠C＝∠DBC＝20°，

∴∠A＝∠C＝20°，

∴∠ABD＝90°∠A＝70°，

∴∠ABC＝∠ABD∠DBC＝70°20°＝50°

故答案为50°．

练习册系列答案
相关题目

【题目】在校园文化艺术节中，九年级一班有1名男生和2名女生获得美术奖，另有2名男生和2名女生获得音乐奖．

（1）从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，求刚好是男生的概率；

（2）分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，用列表或树状图求刚好是一男生一女生的概率．

【题目】年我国个人所得税征收办法最新规定：月收入不超过元的部分不收税；月收入超过元但不超过元的部分征收的所得税；月收入超过元但不超过元的部分征收的所得税国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入（专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用）．如某人月工资收入元，专项附加费支出元，他应缴纳个人所得税为：（元）．

（1）当月收入超过元而又不超过元时，写出应缴纳个人所得税（元）与月收入（元）之间的关系式；

（2）如果某人当月专项附加费支出元，缴纳个人所得税元，那么此人本月工资是多少元？

【题目】如图，在平而直角坐标系中，一次函数y＝﹣4x+4的图象与x轴、y轴分别交于A、B两点．正方形ABCD的项点C、D在第一象限，顶点D在反比例函数y＝（k≠0）的图象上．若正方形ABCD向左平移n个单位后，顶点C恰好落在反比例函数的图象上，则n的值是（　　）

A.2B.3C.4．D.5

【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目，参赛选手以家庭为单位，每组家庭由爸爸妈妈和宝宝3人组成，爸爸、妈妈和宝宝分散在三块区域，选手需在宝宝中选一个宝宝，然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母，不考虑其他因素，仅从数学角度思考，已知在本期比赛中有A、B、C三组家庭进行比赛.

（1）若机器人智能小度选择A组家庭的宝宝，求小度在妈妈区域中正确找出其妈妈的概率；

（2）如果任选一个宝宝（假如选A组家庭），通过列表或树状图的方法，求机器人智能小度至少正确找对宝宝父母其中一人的概率．

【题目】如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D，E两点分别在AC，BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转，记旋转角为α．

（1）问题发现：当α＝0°时，的值为　 　；

（2）拓展探究：当0°≤α＜360°时，若△EDC旋转到如图2的情况时，求出的值；

（3）问题解决：当△EDC旋转至A，B，E三点共线时，若设CE＝5，AC＝4，直接写出线段BE的长　 　．

【题目】某校根据学校实际，决定开设：篮球、：乒乓球、：声乐、：健美操四种活动项目（必选且只能选一个），为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果整理后会制成如图所示的不完整的统计图．请你根据图中提供的信息回答下列问题：

（1）求这次被调查的学生共有多少人；

（2）通过计算补全条形统计图；

（3）已知该校有学生1600人，请根据调查结果估计该校最喜欢乒乓球的学生人数．

【题目】如图，线段AC=n+1（其中n为正整数），点B在线段AC上，在线段AC同侧作正方形ABMN及正方形BCEF，连接AM、ME、EA得到△AME．当AB=1时，△AME的面积记为S1；当AB=2时，△AME的面积记为S2；当AB=3时，△AME的面积记为

S3；则S3﹣S2= ．

【题目】如图，已知一次函数y＝kx+b（k≠0）的图象与x轴、y轴分别交于点A、B两点，且与反比例函数y＝的图象在第一象限内的部分交于点C，CD垂直于x轴于点D，其中OA＝OB＝OD＝2．

（1）直接写出点A、C的坐标；

（2）求这两个函数的表达式；

（3）若点P在y轴上，且S△ACP＝14，求点P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网