题目内容
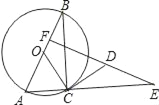
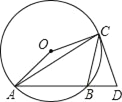
【题目】如图,点A、B、C均在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠ACB=45°,∠AOC=150°.
(1)求证:CD=CB;
(2)⊙O的半径为![]() ,求AC的长.
,求AC的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)延长AO交⊙O于E点,连接CE,由题意可求∠E=75°,∠OAC=∠OCA=15°,∠OCD=90°,根据圆的内接四边形对角互补,以及三角形内角和定理可得∠D=∠CBD=75°,即可证CD=CB;
(2)连接OB,过点B作BF⊥AC于点F,由OA=OB,可得∠OAB=∠OBA=45°,即可求∠AOB=90°,根据勾股定理可求AB的长,AF的长,CF的长,即可求AC的长.
(1)证明:延长AO交⊙O于E点,连接CE
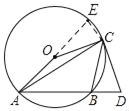
∵AE是直径
∴∠ACE=90°
∵∠ACB=45°
∴∠BCE=135°
∵AO=OC=EO,∠AOC=150°
∴∠OAC=∠OCA=15°,∠OEC=∠OCE=75°
∵四边形ABCE是圆内接四边形
∴∠EAB+∠ECB=180°,∠E+∠ABC=180°
∴∠EAB=45°,∠ABC=105°,
∴∠CAD=30°,∠CBD=75°
∵CD是⊙O切线,
∴∠OCD=90°
∵∠OCA=15°,∠ACB=45°
∴∠CBD=30°
∵∠D+∠CBD+∠BCD=180°
∴∠D=75°
∴∠D=∠CBD
∴CD=CB
(2)连接OB,过点B作BF⊥AC于点F,
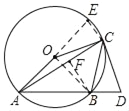
∵OA=OB
∴∠OAB=∠OBA=45°
∴∠AOB=90°
∴AB=![]() =2
=2
∵∠CAD=30°,BF⊥AC
∴BF=1,AF=![]() BF=
BF=![]()
∵∠ACB=45°,BF⊥AC
∴∠ACB=∠CBF=45°
∴CF=BF=1
∴AC=![]() +1
+1

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目