题目内容
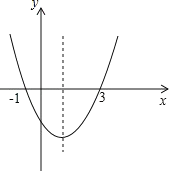
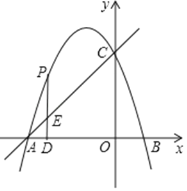
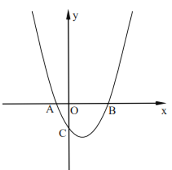
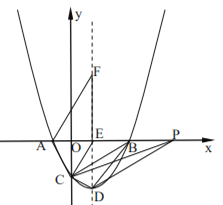
【题目】在平面直角坐标系中(如图),已知抛物线![]() 与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).
与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-2).
(1)求该抛物线的表达式,并写出其对称轴
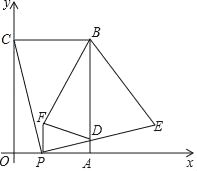
(2)点E为该抛物线的对称轴与x轴的交点,点F在对称轴上,四边形ACEF为梯形,求点F的坐标
(3)点D为该抛物线的顶点,设点P(t, 0),且t>3,如果△BDP和△CDP的面积相等,求t的值.
【答案】(1)![]() ,对称轴为直线x=1;(2)点F的坐标是(1,4);(3)t的值为5
,对称轴为直线x=1;(2)点F的坐标是(1,4);(3)t的值为5
【解析】
(1)根据待定系数法可求抛物线的表达式,进一步得到对称轴即可;
(2)因为AC与EF不平行,且四边形ACEF为梯形,所以有CE∥AF,得到∠FAE=∠OEC,利用tan∠FAE=tan∠OEC,即可求出EF,得到点F的坐标;
(3)计算出抛物线的顶点坐标,以及抛物线与x轴的另一个交点B的坐标,根据t﹥3,得出得点P在点B的右侧,表达出S△BPD与S△CDP,列出方程即可求出t的值.
解:(1)点A(-1,0)和点C(0,-2)在抛物线![]() 上,
上,
∴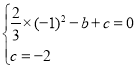 ,解得
,解得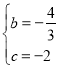
∴该抛物线的表达式为:![]()
该抛物线的对称轴为直线x=1
(2)∵点E为该抛物线对称轴与x轴的交点,
∴E(1,0)
∵AC与EF不平行,四边形ACEF为梯形,AC与y轴的交点为点C,
∴AF∥CE,
∴∠FAE=∠OEC
在Rt△AEF中,∠AEF=90°,![]()
在Rt△OEC中,![]() ,
,
∴![]() .
.
∵OC=2,OE=1,AE=2,
∴![]() ,
,
解得EF=4
∴点F的坐标是(1,4)
(3)∵![]() ,
,
∴抛物线的顶点D的坐标是![]() ,
,
∵点A(-1,0),
∴抛物线与x轴的另一个交点B的坐标(3,0)
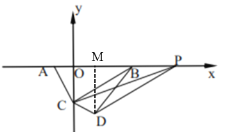
由点P(t,0),且t﹥3,得点P在点B的右侧,
![]()
过点D作DM⊥x轴于点M,
则![]() ,
,
即![]()
∵![]() ,
,
∴t=5
即符合条件的t的值为5.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目