题目内容
【题目】已知△ABC是等边三角形,点P在射线AC上(点P与点A、点C不重合),点D在线段BC的延长线上,且AP=CD,△PCD′与△PCD关于直线AC对称.
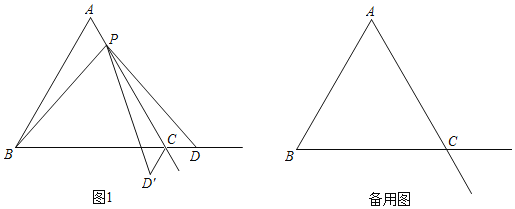
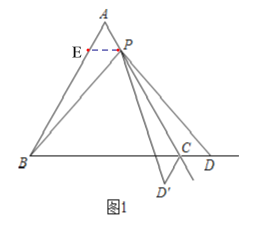
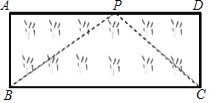
(1)如图1,当点P在线段AC上时,
①求证:PB=PD;
②请求出∠BPD′的度数;
(2)当点P在射线AC上运动时,请直接回答:
①PB=PD是否仍然成立?
②∠BPD′的度数是否发生变化?
(3)将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能否重合?若能重合,请直接写出旋转的角度;若不能重合,请说明理由;
(4)若AB=4,当点P为AC边的中点时,请直接写出PD'的长
【答案】(1)①见解析;②60°;(2)①成立,理由见解析;②∠BPD′的度数不发生变化,理由见解析;(3)PD′与PB能重合,旋转的角度为60°;(4)PD'=2![]()
【解析】
(1)①过点P作PE∥BC交AB于E,易证△APE是等边三角形,得AP=PE,BE=PC,∠BEP=∠PCD,从而得:△BPE≌△PDC,即可得到结论;②由△BPE≌△PDC,得∠PBE=∠DPC,进而得∠PBE=∠D'PC,由∠BPC=∠A+∠PBE=60°+∠D'PC,即可得到结论;
(2)①过点P作PE∥BC交AB的延长线于E,易证△APE是等边三角形,得AP=PE,BE=PC,∠BEP=∠PCD=60°,得△BPE≌△PDC(SAS),即可得到结论;②由△BPE≌△PDC,得∠PBE=∠DPC,进而得∠PBE=∠D'PC,即可得到结论.
(3)由(1)(2)知,∠BPD'=60°,PB=PD=PD',即可得到结论;
(4)由△ABC是等边三角形,点P是AC的中点,得AP=2,BP⊥AC,根据勾股定理得BP的值,进而即可得到答案.
(1)①∵△ABC是等边三角形,
∴AB=AC,∠A=∠ABC=∠ACB=60°,
过点P作PE∥BC交AB于E,如图1,
∴∠AEP=∠ABC=60°,∠APE=∠ACB=60°,
∴∠AEP=∠APE=∠A=60°,
∴△APE是等边三角形,
∴AP=PE,
∴AB﹣AE=AC﹣AP,
∴BE=PC,
∵AP=CD,
∴PE=CD,
∵∠BEP=180°﹣∠AEP=120°,∠PCD=180°﹣∠ACB=120°,
∴∠BEP=∠PCD,
∴△BPE≌△PDC(SAS),
∴PB=PD;
②由①知,△BPE≌△PDC,
∴∠PBE=∠DPC,
∵△PCD′与△PCD关于直线AC对称,
∴∠DPC=∠D'PC,
∴∠PBE=∠D'PC,
∵∠BPC=∠A+∠PBE=60°+∠D'PC,
∴∠BPD'=∠BPC﹣∠D'PC=60°;
(2)①PB=PD仍然成立,理由如下:
∵△ABC是等边三角形,
∴AB=AC,∠A=∠ABC=∠ACB=60°,
∴∠DCP=60°
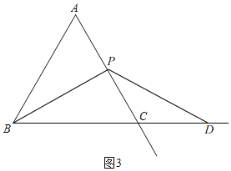
过点P作PE∥BC交AB的延长线于E,如图2,
∴∠AEP=∠ABC=60°,∠APE=∠ACB=60°,
∴∠AEP=∠APE=∠A=60°,
∴△APE是等边三角形,
∴AP=PE,
∴AE﹣AB=AP﹣AC,
∴BE=PC,
∵AP=CD,
∴PE=CD,
∵∠BEP=∠PCD=60°
∴△BPE≌△PDC(SAS),
∴PB=PD;
②∠BPD′的度数不发生变化,理由如下:
由①知,△BPE≌△PDC,
∴∠PBE=∠DPC,
∵△PCD′与△PCD关于直线AC对称,
∴∠DPC=∠D'PC,
∴∠PBE=∠D'PC,
∴∠BPD'=∠D'PC﹣∠BPC=∠PBE﹣∠BPC
=∠PBE﹣(∠APE﹣∠BPE)
=∠PBE﹣(60°﹣∠BPE)
=∠PBE+∠BPE﹣60°
=180°﹣∠AEP﹣60°
=180°﹣60°﹣60°
=60°;
(3)∵由(1)(2)知,∠BPD'=60°,PB=PD=PD',
∴将△PCD′绕点P顺时针旋转,在旋转的过程中,PD′与PB能重合,
∴旋转的角度为60°;
(4)如图3,由(1)知,BP=PD,由对称得,PD=PD',
∴BP=PD',
∵△ABC是等边三角形,点P是AC的中点,
∴AP=![]() AC=
AC=![]() AB=2,BP⊥AC,
AB=2,BP⊥AC,
∴∠APB=90°,
在Rt△ABP中,根据勾股定理得,BP=![]() ,
,
∴PD'=2![]() .
.