题目内容
【题目】已知:在⊙O中,弦AC⊥弦BD,垂足为H,连接BC,过点D作DE⊥BC于点E,DE交AC于点F.
(1)如图1,求证:BD平分∠ADF;
(2)如图2,连接OC,若OC平分∠ACB,求证:AC=BC;
(3)如图3,在(2)的条件下,连接AB,过点D作DN∥AC交⊙O于点N,若tan∠ADB=![]() ,AB=3
,AB=3![]() ,求DN的长.
,求DN的长.



【答案】(1)证明见解析;(2)证明见解析;(3)9.
【解析】试题分析:(1)先根据同角的余角相等可证得: ∠ACB=∠BDE,再根据同弧所对的圆周角相等可得: ∠ACB=∠ADB,所以∠BDE=∠ADB,所以BD平分∠ADF,(2)连接OB,OA,则
△AOC,△BOC是等腰三角形,再证△AOC≌△BOC,根据全等三角形的性质可得:AC=BC,
(3)根据∠ACB=∠ADB, tan∠ADB=![]() ,所以tan∠ACB=
,所以tan∠ACB=![]() ,所以
,所以![]() ,可设BH=3x,CH=4x,由勾股定理可得:BC=5x,则AC=5x,所以AH=x,根据勾股定理可得:
,可设BH=3x,CH=4x,由勾股定理可得:BC=5x,则AC=5x,所以AH=x,根据勾股定理可得: ![]() ,因为AB=
,因为AB=![]() ,所以可得:
,所以可得: ![]() ,
,![]() ,解得:x=3,所以DH=4,CH=12,BH=9,BC=15,
,解得:x=3,所以DH=4,CH=12,BH=9,BC=15,
所以BD=13,由相似三角形性质可得:BN=![]() ,再根据勾股定理解得: DN=9.
,再根据勾股定理解得: DN=9.
试题解析:(1) 因为弦AC⊥弦BD, DE⊥BC于点E,
所以∠ACB+∠DBE=∠BDE+∠DBE=90°,
所以∠ACB=∠BDE,
又因为∠ACB=∠ADB,
所以∠BDE=∠ADB,
所以BD平分∠ADF,
(2) 连接OB,OA,则△AOC,△BOC是等腰三角形,
所以∠OCB=∠OBC, ∠OAC=∠OCA,
又因为OC平分∠ACB,
所以∠OCB==∠OCA,
所以∠OBC=∠OAC,
在△AOC和△BOC中,
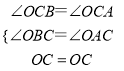 ,
,
所以△AOC≌△BOC,
所以AC=BC,
(3)因为∠ACB=∠ADB, tan∠ADB=![]() ,
,
所以tan∠ACB=![]() ,所以
,所以![]() ,可设BH=3x,CH=4x,由勾股定理得:BC=5x,
,可设BH=3x,CH=4x,由勾股定理得:BC=5x,
则AC=5x,所以AH=x,
因为AB=![]() ,根据勾股定理得:
,根据勾股定理得: ![]() ,
,
所以得: ![]() ,
,![]() ,解得:x=3,
,解得:x=3,
所以BC=15,
设等腰△ACB底边AB上的高为h,由勾股定理可得: ![]() ,
,
根据相似三角形性质可得: ![]() ,即
,即 ,解得BN=
,解得BN=![]() ,
,
根据勾股定理可得:DN=![]() =
=![]() .
.






