题目内容
【题目】四边形ABCD为菱形,BD为对角线,在对角线BD上任取一点E,连接CE,把线段CE绕点C顺时针旋转得到线段CF,使得∠ECF=∠BCD ,点E的对应点为点F,连接DF.
(1)如图1,求证:BE=DF;
(2)如图2,若DF=![]() CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.
CF=10, ∠DFC=2∠BDC,求菱形ABCD的边长.


【答案】(10证明见解析;(2)![]() .
.
【解析】试题分析:(1)先根据∠ECF=∠BCD,可求证∠ECB=∠DCF,由旋转可得:EC=FC,由菱形的性质可得:BC=CD,根据SAS可证△BCE≌△DCF,所以BE=DF,(2)根据DF=![]() CF=10,可得DF=10,CF=4,由 ∠DFC=2∠BDC,可得: ∠BEF=2∠BDC,根据三角形的性质性质可得:
CF=10,可得DF=10,CF=4,由 ∠DFC=2∠BDC,可得: ∠BEF=2∠BDC,根据三角形的性质性质可得:
∠BEF=∠BDC+∠ECD,所以∠BDC=∠ECD,所以BE=CE=CF=4,所以BD=14,利用相似三角形的判定可证△BCD∽△CED,根据相似三角形的性质可得: ![]() ,然后计算可得DC.
,然后计算可得DC.
试题解析:(1)因为∠ECF=∠BCD,
所以∠ECF-∠ECD=∠BCD-∠ECD,
所以∠ECB=∠DCF,
由旋转可得: EC=FC,
因为菱形ABCD,
所以BC=CD,
在△BCE和△DCF中,
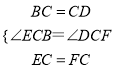 ,
,
所以△BCE≌△DCF,
所以BE=DF,
(2)因为DF=![]() CF=10,所以DF=10,CF=4,
CF=10,所以DF=10,CF=4,
因为∠DFC=2∠BDC,所以 ∠BEF=2∠BDC,
又因为∠BEF=∠BDC+∠ECD,
所以∠BDC=∠ECD,
所以BE=CE=CF=4,所以BD=14,
因为△BCD和△CED是等腰三角形,且∠BDC是公共角
所以△BCD∽△CED,所以![]() ,即
,即![]() ,解得CD=
,解得CD=![]() ,
,
所以菱形的边长为![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目