题目内容
 (2012•槐荫区二模)如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数y=
(2012•槐荫区二模)如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数y=| k | x |
(1)求反比例函数的函数解析式及点F的坐标;
(2)你认为线段OE与CF有何位置关系?请说明你的理由.
(3)求证:AM=AO.
分析:(1)求出E的坐标,求出反比例函数的解析式,把x=4代入即可求出F的坐标;
(2)证△OCE≌△CBF,推出∠COE=∠BCF,求出∠ECF+∠CEO=90°即可;
(3)过M作MN⊥OC于N,证△CMO和△ECO相似,求出CM、OM,根据三角形的面积公式求出MN,根据勾股定理求出ON,得出M的坐标,根据勾股定理求出AM的值即可.
(2)证△OCE≌△CBF,推出∠COE=∠BCF,求出∠ECF+∠CEO=90°即可;
(3)过M作MN⊥OC于N,证△CMO和△ECO相似,求出CM、OM,根据三角形的面积公式求出MN,根据勾股定理求出ON,得出M的坐标,根据勾股定理求出AM的值即可.
解答:(1)解:∵正方形ABCO,B(4,4),E为BC中点,
∴OA=AB=BC=OC=4,CE=BE=2,F的横坐标是4,
∴E的坐标是(2,4),
把E的坐标代入y=
得:k=8,
∴y=
,
∵F在双曲线上,
∴把F的横坐标是4代入得:y=2,
∴F(4,2),
答:反比例函数的函数解析式是y=
,点F的坐标是(4,2).
(2)线段OE与CF的位置关系是OE⊥CF,
理由是:∵E的坐标是(2,4),点F的坐标是(4,2),
∴AF=4-2=2=CE,
∵正方形OABC,
∴OC=BC,∠B=∠BCO=90°,
∵在△OCE和△CBF中
,
∴△OCE≌△CBF,
∴∠COE=∠BCF,
∵∠BCO=90°,
∴∠COE+∠CEO=90°,
∴∠BCF+∠CEO=90°,
∴∠CME=180°-90°=90°,
即OE⊥CF.
(3)证明:∵OC=4,CE=2,由勾股定理得:OE=2
,
过M作MN⊥OC于N,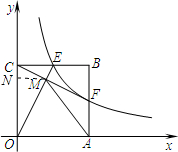
∵OE⊥CF,
∴∠CMO=∠OCE=90°,
∵∠COE=∠COE,
∴△CMO∽△ECO,
∴
=
=
,
即
=
=
,
解得:CM=
,OM=
,
在△CMO中,由三角形的面积公式得:
×OC×MN=
×CM×OM,
即4MN=
×
,
解得:MN=
,
在△OMN中,由勾股定理得:ON=
=
,
即M(
,
),
∵A(4,0),
∴由勾股定理得:AM=4=AO,
即AM=AO.
∴OA=AB=BC=OC=4,CE=BE=2,F的横坐标是4,
∴E的坐标是(2,4),
把E的坐标代入y=
| k |
| x |
∴y=
| 8 |
| x |
∵F在双曲线上,
∴把F的横坐标是4代入得:y=2,
∴F(4,2),
答:反比例函数的函数解析式是y=
| 8 |
| x |
(2)线段OE与CF的位置关系是OE⊥CF,
理由是:∵E的坐标是(2,4),点F的坐标是(4,2),
∴AF=4-2=2=CE,
∵正方形OABC,
∴OC=BC,∠B=∠BCO=90°,
∵在△OCE和△CBF中
|
∴△OCE≌△CBF,
∴∠COE=∠BCF,
∵∠BCO=90°,
∴∠COE+∠CEO=90°,
∴∠BCF+∠CEO=90°,
∴∠CME=180°-90°=90°,
即OE⊥CF.
(3)证明:∵OC=4,CE=2,由勾股定理得:OE=2
| 5 |
过M作MN⊥OC于N,

∵OE⊥CF,
∴∠CMO=∠OCE=90°,
∵∠COE=∠COE,
∴△CMO∽△ECO,
∴
| OC |
| OE |
| CM |
| CE |
| OM |
| OC |
即
| 4 | ||
2
|
| CM |
| 2 |
| OM |
| 4 |
解得:CM=
4
| ||
| 5 |
8
| ||
| 5 |
在△CMO中,由三角形的面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
即4MN=
4
| ||
| 5 |
8
| ||
| 5 |
解得:MN=
| 8 |
| 5 |
在△OMN中,由勾股定理得:ON=
| OM2-MN2 |
| 16 |
| 5 |
即M(
| 8 |
| 5 |
| 16 |
| 5 |
∵A(4,0),
∴由勾股定理得:AM=4=AO,
即AM=AO.
点评:本题考查了用待定系数法求反比例函数的解析式,勾股定理,相似三角形的性质和判定,全等三角形的性质和判定等知识点的运用,能综合运用这些性质进行推理和计算是解此题的关键,本题综合性比较强,有一定的难度.

练习册系列答案
相关题目