题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为 . 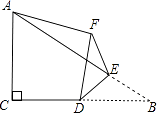
【答案】![]()
【解析】解:由题意得:DF=DB,
∴点F在以D为圆心,BD为半径的圆上,作⊙D; 连接AD交⊙D于点F,此时AF值最小,
∵点D是边BC的中点,
∴CD=BD=3;而AC=4,
由勾股定理得:AD2=AC2+CD2
∴AD=5,而FD=3,
∴FA=5﹣3=2,
即线段AF长的最小值是2,
连接BF,过F作FH⊥BC于H,
∵∠ACB=90°,
∴FH∥AC,
∴△DFH∽△ADC,
∴ ![]() ,
,
∴HF= ![]() ,DH=
,DH= ![]() ,
,
∴BH= ![]() ,
,
∴BF= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.

【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?