��Ŀ����
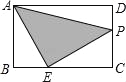
����Ŀ����ͼ����Rt��ABC�У���C��90��AB��10cm��AC��BC��4��3����P�ӵ�A������AB�������B�˶����ٶ�Ϊ1cm/s��ͬʱ��Q�ӵ�B������B��C��A�������A�˶����ٶ�Ϊ2cm/s����һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶���
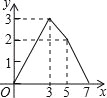
��1�����P���˶�ʱ��Ϊx���룩����PBQ�����Ϊy��cm2��������PBQ����ʱ����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����x��5��ʱ����ֱ��PQ���Ƿ����һ��M��ʹ��BCM���ܳ���С�������ڣ������С�ܳ����������ڣ���˵�����ɣ�
��3������Q��BC�����˶�ʱ���Ƿ����x��ʹ������PBQ��һ������ΪԲ����Բʱ��������������������Բ�ϣ������ڣ���� x��ֵ�������ڣ�˵������.

���𰸡�(1)��y=��![]() ��8x��0��x��3����y=
��8x��0��x��3����y=![]() ��(2)��16��(3)��x=
��(2)��16��(3)��x=![]() .
.
��������
���������(1)���ֵ�Q�ڱ�BC�Ϻ͵�Q�ڱ�CA���˶���(2)������AQ=14��2x=14��10=4��AP=x=5�Լ�AC=8��AB=10���Ӷ��ó�PQ��AC�Ĵ�ֱƽ���ߣ���PC=AP=5��������M��P�غ�ʱ����BCM���ܳ���С��(3)��������Ҫ����������ó���.
���������(1)��������Q�ڱ�BC���˶�ʱ��y=��![]() ��8x��0��x��3����
��8x��0��x��3����
������Q�ڱ�CA���˶�ʱ��y=![]() =
=![]() ��3��x��7����
��3��x��7����

(2)�����ڣ� ���ɣ���AQ=14��2x=14��10=4��AP=x=5�� ��AC=8��AB=10��
��PQ����ABC����λ�ߣ� ��PQ��AB����PQ��AC�� ��PQ��AC�Ĵ�ֱƽ���ߣ�
��PC=AP=5�� ������M��P�غ�ʱ����BCM���ܳ���С��
���BCM���ܳ�Ϊ�� MB��BC��MC��PB��BC��PC=5��6��5=16�� ���BCM���ܳ���СֵΪ16��
(3)�����������PBQ����������
��PQ=PB,x=![]() ��3(��) ��BQ=BP��x=
��3(��) ��BQ=BP��x=![]() ��3���ᣩ ��QP=QB,x=
��3���ᣩ ��QP=QB,x=![]() ��
��
�����������������������x��x=![]() .
.

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�