题目内容
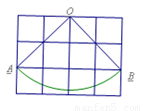
 如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面积为
如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面积为| π |
| 2 |
| π |
| 2 |
分析:利用勾股定理的逆定理即可求得扇形的圆心角,然后利用弧长公式求得扇形的弧长,即圆锥的底面周长,根据圆的周长公式求得底面圆的半径,则面积即可求得.
解答:解:根据勾股定理可以得到:OA2=OB2=22+22=4+4=8,即OA=2
.
∵AB=4,42=8+8
即AB2=OA2+OB2.
∴△OAB是等腰直角三角形.
∴
的长是
=
π.
设圆锥的底面半径是r,则2πr=
π,
解得:r=
.
则圆锥的底面面积是:π(
)2=
.
故答案是:
.
| 2 |
∵AB=4,42=8+8
即AB2=OA2+OB2.
∴△OAB是等腰直角三角形.
∴
 |
| AB |
90π×2
| ||
| 180 |
| 2 |
设圆锥的底面半径是r,则2πr=
| 2 |
解得:r=
| ||
| 2 |
则圆锥的底面面积是:π(
| ||
| 2 |
| π |
| 2 |
故答案是:
| π |
| 2 |
点评:考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 (2013•椒江区一模)我们把弧长等于半径的扇形叫等边扇形.如图,扇形OAB是等边扇形,设OA=R,下列结论中:①∠AOB=60°;②扇形的周长为3R;③扇形的面积为
(2013•椒江区一模)我们把弧长等于半径的扇形叫等边扇形.如图,扇形OAB是等边扇形,设OA=R,下列结论中:①∠AOB=60°;②扇形的周长为3R;③扇形的面积为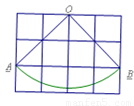
 ;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )
;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )
 ;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )
;④点A与半径OB中点的连线垂直OB;⑤设OA、OB的垂直平分线交于点P,以P为圆心,PA为半径作圆,则该圆一定会经过扇形的弧AB的中点.其中正确的个数为( )