题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B
(1)求抛物线的解析式;
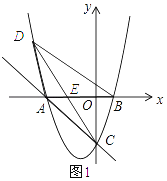
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD=![]() S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标;
(3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
【答案】(1)y=x2+2x﹣3(2)(﹣4,5)(3)3+![]()
【解析】试题分析:(1)、首先求出点A和点C的坐标,然后将其代入二次函数解析式,利用待定系数法求出函数解析式;(2)、首先求出AB的长度,然后根据面积之间的关系得出点E的坐标,从而得出直线CE的函数解析式,将一次函数和二次函数联立成方程组,从而得出点D的坐标;(3)、过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M,利用待定系数法求出直线BC和直线DE的函数解析式,从而求出点E的坐标,利用两点之间的距离公式得出BC和CE的长度,证明出△PCB和△QEB全等,将y=3代入二次函数解析式,从而得到点F的坐标,最后求出EF的长度.
试题解析:(1)解:∵令x=0得:y=﹣3, ∴C(0,﹣3).
令y=0得:﹣x﹣3=0,解得x=﹣3, ∴A(﹣3,0).
将A、C两点的坐标代入抛物线的解析式的: ![]() ,解得:
,解得: ![]() .
.
∴抛物线的解析式为y=x2+2x﹣3
(2)解:如图1所示: 令y=0得:x2+2x﹣3=0,解得x=﹣3或x=1. ∴AB=4.
∵S△ACD= ![]() S四边形ACBD , ∴S△ADC:S△DCB=3:5. ∴AE:EB=3:5. ∴AE=4×
S四边形ACBD , ∴S△ADC:S△DCB=3:5. ∴AE:EB=3:5. ∴AE=4× ![]() =
= ![]() .
.
∴点E的坐标为(﹣ ![]() ,0).
,0).
设EC的解析式为y=kx+b,将点C和点E的坐标代入得: ![]() ,
,
解得:k=﹣2,b=﹣3. ∴直线CE的解析式为y=﹣2x﹣3.
将y=﹣2x﹣3与y=x2+2x﹣3联立,解得:x=﹣4或x=0(舍去),
将x=﹣4代入y=﹣2x﹣3得:y=5, ∴点D的坐标为(﹣4,5).
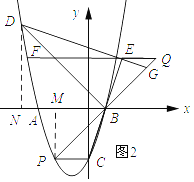
(3)解:如图2所示:过点D作DN⊥x轴,垂足为N,过点P作PM⊥x轴,垂足为M.
设直线BC的解析式为y=kx+b,将点C和点B的坐标代入得: ![]() ,
,
解得:k=3,b=﹣3, ∴直线BC的解析式为y=3x﹣3.
设直线DE的解析式为y=﹣ ![]() x+n,将点D的坐标代入得:﹣
x+n,将点D的坐标代入得:﹣ ![]() ×(﹣4)+n=5,
×(﹣4)+n=5,
解得:n=5﹣ ![]() =
= ![]() . ∴直线DE的解析式为y=﹣
. ∴直线DE的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
将y=3x﹣3与y=﹣ ![]() x+
x+ ![]() 联立解得:x=2,y=3. ∴点E坐标为(2,3).
联立解得:x=2,y=3. ∴点E坐标为(2,3).
依据两点间的距离公式可知:BC=CE= ![]() .
.
∵点P与点Q关于点B对称, ∴PB=BQ.
在△PCB和△QEB中 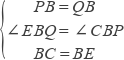 , ∴△PCB≌△QEB.
, ∴△PCB≌△QEB.
∴∠BPC=∠Q. 又∵∠DEF+∠BPC=∠DBE,∠DEF=∠QEG,∠EGB=∠Q+∠QEG
∴∠DBE=∠DGB. 又∵∠DBE+∠BDE=90°, ∴∠DGB+∠BDG=90°,即∠PBD=90°.
∵D(﹣4,5),B(1,0), ∴DM=NB. ∴∠DBN=45°. ∴∠PBM=45°.
∴PM=MB 设点P的坐标为(a,a2+2a﹣3),则BM=1﹣a,PM=﹣a2﹣2a+3.
∴1﹣a=﹣a2﹣2a+3,解得:a=﹣2或a=1(舍去). ∴点P的坐标为(﹣2,3).
∴PC∥x轴. ∵∠Q=∠BPC, ∴EQ∥PC. ∴点E与点F的纵坐标相同.
将y=3代入抛物线的解析式得:x2+2x﹣3=3,解得:x=﹣1﹣![]() 或x=﹣1+
或x=﹣1+![]() (舍去).
(舍去).
∴点F的坐标为(﹣1 ![]() ,3). ∴EF=2﹣(﹣1﹣
,3). ∴EF=2﹣(﹣1﹣![]() )=3+
)=3+![]() .
.

【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.