题目内容
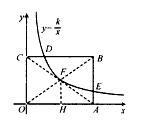
已知:如图,矩形OABC的两边OA、OC分别在x轴,y轴的正半轴上,且点B的坐标为(4,3),反比例函数y=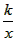 图象与BC交于点D,与AB交于点E,其中点D的坐标为(1,3)。
图象与BC交于点D,与AB交于点E,其中点D的坐标为(1,3)。
(1)求反比例函数的解析式及E点的坐标;
(2)若矩形OABC对角线的交点为F,请判断点F是否在此反比例函数的图象上,并说明理由。
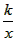 图象与BC交于点D,与AB交于点E,其中点D的坐标为(1,3)。
图象与BC交于点D,与AB交于点E,其中点D的坐标为(1,3)。(1)求反比例函数的解析式及E点的坐标;
(2)若矩形OABC对角线的交点为F,请判断点F是否在此反比例函数的图象上,并说明理由。
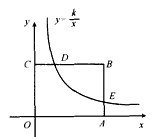
解:(1)把D(1,3)代人y=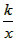 ,得3= ,得3=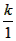 , , ∴k=3, ∴反比例函数的解析式为y= 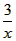 , ,当=4时,y= 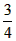 , ,∴E(4, 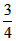 ); ); |
|
| (2)点F在反比例函数的图象上,理由如下: 连接AC,OB交于点F,过F作FH ⊥x轴于H, ∵四边形OABC是矩形, ∴OF=FB= 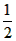 OB, OB,又∵∠FHO=∠BAO=90°,∠FOH=∠BOA, ∴△OFH∽△OBA, ∴OH/OA=FH/BA=OF/OB= 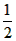 , ,∴OH=2,FH= 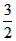 , ,∴F(2, 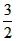 ), ),∵当x=2时,y= 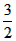 , ,∴点F在反比例函数y= 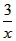 的图象上。 的图象上。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
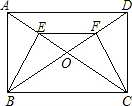 已知:如图,矩形ABCD中,AC和BD交于点O,E、F分别是OA、OD的中点.
已知:如图,矩形ABCD中,AC和BD交于点O,E、F分别是OA、OD的中点.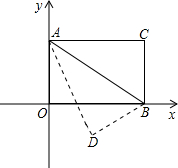 B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.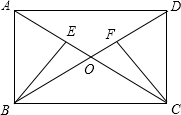 已知:如图,矩形ABCD中,对角线AC与BD交于点O,点E、F分别在OA、OD上,且OE=
已知:如图,矩形ABCD中,对角线AC与BD交于点O,点E、F分别在OA、OD上,且OE=

