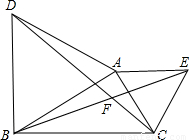
题目内容
已知△ABD和△BEP均为等腰直角△,∠BAD=∠BEP=90゜,点O为BD的中点.
(1)如图,点P、E分别在AB、BD上,求证:AP=
OE;
(2)将图1中的△BPE绕B点顺时针旋转45゜,问(1)中的结论是否成立?请说明理由.

(1)如图,点P、E分别在AB、BD上,求证:AP=
| 2 |
(2)将图1中的△BPE绕B点顺时针旋转45゜,问(1)中的结论是否成立?请说明理由.

分析:(1)根据等腰三角形的两直角边相等,和勾股定理求得BP、OB的值.则易证AP与OE的数量关系;
(2)将图1中的△BPE绕B点顺时针旋转45゜,问(1)中的结论成立,通过证明△BOA∽△BEP,即可得到问题答案.
(2)将图1中的△BPE绕B点顺时针旋转45゜,问(1)中的结论成立,通过证明△BOA∽△BEP,即可得到问题答案.
解答: (1)证明:∵△ABD为等腰直角三角形,∠BAD=∠BEP=90゜,
(1)证明:∵△ABD为等腰直角三角形,∠BAD=∠BEP=90゜,
∴设AB=AD=a,则BD=
a.
又∵点O为BD的中点,
∴OB=
BD=
a.
同理,设EP=BE=b,则BP=
b.
∴AP=AB-BP=a-
b,OE=OB-BE=
a-b,
则
=
=
,
∴AP=
OE;
(2)∵△BEP是等腰直角三角形,
∴∠B=∠BPE=45°,
∵△ABD是等腰直角三角形,O是BD的中点,
∴AO⊥BD,
∴∠BOA=∠BEP=90°,∠BAO=180°-∠BOA-∠B=45°,
∴△BOA∽△BEP,
∵
=
=
,
∴
=
,
∴AP=
OE.
 (1)证明:∵△ABD为等腰直角三角形,∠BAD=∠BEP=90゜,
(1)证明:∵△ABD为等腰直角三角形,∠BAD=∠BEP=90゜,∴设AB=AD=a,则BD=
| 2 |
又∵点O为BD的中点,
∴OB=
| 1 |
| 2 |
| ||
| 2 |
同理,设EP=BE=b,则BP=
| 2 |
∴AP=AB-BP=a-
| 2 |
| ||
| 2 |
则
| AP |
| OE |
a-
| ||||
|
| 2 |
∴AP=
| 2 |
(2)∵△BEP是等腰直角三角形,
∴∠B=∠BPE=45°,
∵△ABD是等腰直角三角形,O是BD的中点,
∴AO⊥BD,
∴∠BOA=∠BEP=90°,∠BAO=180°-∠BOA-∠B=45°,
∴△BOA∽△BEP,
∵
| BP |
| BE |
| BA |
| BO |
| 2 |
∴
| AP |
| OE |
| 2 |
∴AP=
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质以及相似三角形的判定和性质,题目的综合性很强难度不小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
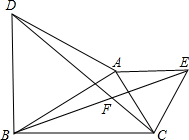 已知△ABD和△ACE都是等边三角形,CD,BE相交于点F.
已知△ABD和△ACE都是等边三角形,CD,BE相交于点F. (2012•江门模拟)如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.
(2012•江门模拟)如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.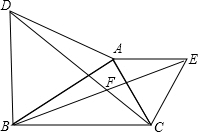 如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.
如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.