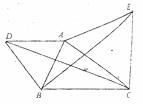
题目内容
如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.(1)求证:△ABE≌△ADC;
(2)△ABE可由△ADC经过怎样的旋转变换得到?
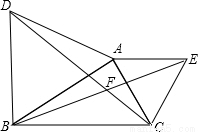
【答案】分析:(1)根据全等三角形的SAS定理,即可证得;因为△ABD和△ACE都是等边三角形,所以有AD=AB,AC=AE,∠DAB=∠EAC=60°,又因为∠DAB+∠BAC=∠EAC+∠BAC,所以∠DAC=∠BAE,故可根据SAS判定△ADC≌△ABE.
(2)由(1)可知,△ABE≌△ADC,只需找出旋转角,即可得出.
解答:(1)证明:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△ABE和△ADC中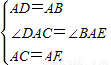 ,
,
△ABE≌△ADC(SAS)
(2)解:△ABE可由△ADC绕A点逆时针旋转60得到的.
点评:本题主要考查了三角形全等的判定方法,以及图形的旋转,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
(2)由(1)可知,△ABE≌△ADC,只需找出旋转角,即可得出.
解答:(1)证明:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△ABE和△ADC中
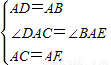 ,
,△ABE≌△ADC(SAS)
(2)解:△ABE可由△ADC绕A点逆时针旋转60得到的.
点评:本题主要考查了三角形全等的判定方法,以及图形的旋转,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 (2012•江门模拟)如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.
(2012•江门模拟)如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F. 如图,已知△ABD和△ACE,AD=AE,∠1=∠2,要判定△ABD≌△ACE,还需要添加一个条件,这个条件可以是
如图,已知△ABD和△ACE,AD=AE,∠1=∠2,要判定△ABD≌△ACE,还需要添加一个条件,这个条件可以是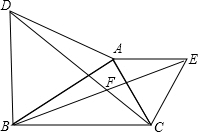 如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.
如图,已知△ABD和△ACE都是等边三角形,CD、BE相交于点F.