题目内容
21、如图,已知线段AB=6,延长线段AB到C,使BC=2AB,点D是AC的中点.
求:(1)AC的长;(2)BD的长.
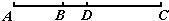
求:(1)AC的长;(2)BD的长.
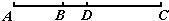
分析:由已知条件可知,BC=2AB,AB=6,则BC=12,故AC=AB+BC可求;又因为点D是AC的中点,则AD=$frac{1}{2}$AC,故BD=BC-DC可求.
解答:解:(1)∵BC=2AB,AB=6,
∴BC=12,
∴AC=18;
(2)D是AC的中点,AC=18,
∴AD=9,
∴BD=BC-DC=12-9=3.
故答案为18、3.
∴BC=12,
∴AC=18;
(2)D是AC的中点,AC=18,
∴AD=9,
∴BD=BC-DC=12-9=3.
故答案为18、3.
点评:做这类题时一定要与图形结合,这样才直观形象,不易出错.利用中点性质转化线段之间的倍分关系是解题的关键.

练习册系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


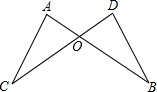 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.