题目内容
【题目】已知直线y=
x+2与y轴交于点A，与双曲线y=
有一个交点为B（2，3），将直线AB向下平移，与x轴.y轴分别交于点C，D，与双曲线的一个交点为P，若
，则点D的坐标为________．
【答案】（0，
）或（0，-）或（0，
）或（0，-）．
【解析】
设D的坐标为（0，m），根据平行线分线段成比例定理得出
，然后根据
，求得PM的值，从而求得P的坐标，代入直线解析式即可求得m的值．
当D点在y轴的正半轴时，如图1所示，
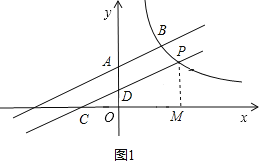
设D的坐标为（0，m），
∵将直线AB向下平移，与x轴、y轴分别交于点C，D，
∴CD∥AB，
∴直线CD的解析式为y=
x+m，
作PM⊥x轴于M，
∴PM∥y轴，
①P在第一象限时，，
∵，
∴
，
∴PM=3OD=3m，
∵P是双曲线的一个交点，
∴P（
，3m），
∴3m=×+m，
解得m=±，
∴m＞0，
∴D（0，）；
②P在第三象限时，，
∵，
∴
，
∴PM=OD=m，
∵P是双曲线的一个交点，
∴P（-
，-m），
∴-m=×（-）+m，
解得m=±，
∴m＞0，
∴D（0，）；
当D点在y轴的负半轴时，如图2所示，
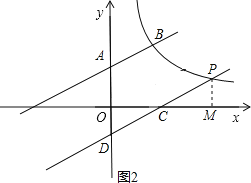
作PM⊥x轴于M，
∴PM∥y轴，
③P在第一象限时，，
∵，
∴，
∴PM=OD=m，
∵P是双曲线的一个交点，
∴P（-，-m），
∴-m=×（-）+m，
解得m=±，
∴m＜0，
∴D（0，-）；
④P在第三象限时，，
∵，
∴，
∴PM=3OD=3m，
∵P是双曲线的一个交点，
∴P（，3m），
∴3m=×+m，
解得m=±，，
∴m＜0，
∴D（0，-）；
综上，点D的坐标为（0，）或（0，-）或（0，）或（0，-），
故答案为：（0，）或（0，-）或（0，）或（0，-）．
练习册系列答案
相关题目
