题目内容
【题目】将从1开始的连续自然数按图规律排列：规定位于第3行，第2列的自然数10记为（3，2），自然数15记为（4，2）……．
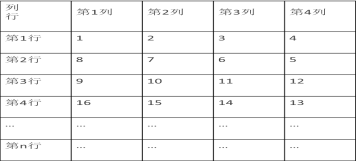
按此规律，回答下列问题：
（1）记为（6，3）表示的自然数是___________；
（2）自然数2018记为 __________；
（3）用一个正方形方框在第3列和第4列中任意框四个数，这四个数的和能为2018吗？如果能，求出框出的四个数中最小的数；如果不能，请写出理由．
【答案】（1）22；（2）（505，2）；(3)见解析.
【解析】
(1)由图表可知每4个数一循环，奇数行从左往右依次增加，偶数行从右往左依次增加，根据规律，算出(6，3)即可；
(2)根据规律，用2018除以8，利用商和余数判定行数与列数即可；
(3)根据规律，可知框出的四个数由小到大各相差1或者是与最小数相差1、6、7这两种情况，分别求出后进行判断即可.
(1)由图表可知两行每8个数一循环，奇数行从左往右依次增加，偶数行从右往左依次增加，根据规律，第5 行最后一个(5，4)为20，第6行最后一个(6，4)为21，
(6，3)为22，
故答案为：22；
(2)
，
位于第252×2+1=505行，第2列，
故答案为：(505，2)；
(3)设框出的四个数中最小的数为
，则其它的三个数分别为：
，
，
或，
，
，
依题意得：
或
，
解得：
或
，
501是第126行第4列的数，503是126行第2列的数，
∵503是第2列中的数,不合题意,舍去，
∴框出的四个数中最小的数为501．
【题目】为响应我市“中国梦”“宜宾梦”主题教育活动，某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛，评选出一、二、三等奖和优秀奖．小明同学根据获奖结果，绘制成如图所示的统计表和数学统计图．
等级 | 频数 | 频率 |
一等奖 | a | 0.1 |
二等奖 | 10 | 0.2 |
三等奖 | b | 0.4 |
优秀奖 | 15 | 0.3 |
请你根据以上图表提供的信息，解答下列问题：
（1）a= ， b= ， n= ．
（2）学校决定在获得一等奖的作者中，随机推荐两名作者代表学校参加市级比赛，其中王梦、李刚都获得一等奖，请用画树状图或列表的方法，求恰好选中这二人的概率．
