题目内容
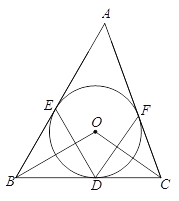
【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F, ![]() ,
, ![]() .
.
(1)求∠BOC的度数;
(2)求∠EDF的度数.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由切线长定理可知BO,CO分别是∠ABC和∠ACB的角平分线,则∠OBC和∠OCB的度数可求出,进而可求出∠BOC的度数;
(2)连接OE,OF.由三角形内角和定理可求得∠A=50°,由切线的性质可知:∠OFA=90°,∠OEA=90°,从而得到∠A+∠EOF=180°,故可求得∠EOF=130°由圆周角定理可求得∠EDF=65°.
试题解析:(1)∵⊙O是△ABC的内切圆,切点分别为D、E、F,
∴BO,CO分别是∠ABC和∠ACB的角平分线,
∴∠OBC=![]() ∠ABC=30°,∠OCB=
∠ABC=30°,∠OCB=![]() ∠ACB=35°,
∠ACB=35°,
∴∠BOC=180°﹣30°﹣35°=115°;
(2)如图所示;连接OE,OF.
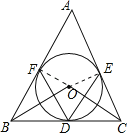
∵∠ABC=60°,∠ACB=70°,
∴∠A=180°﹣60°﹣70°=50°.
∵AB是圆O的切线,
∴∠OFA=90°.
同理∠OEA=90°.
∴∠A+∠EOF=180°.
∴∠EOF=130°.
∴∠EDF=65°.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目


