题目内容
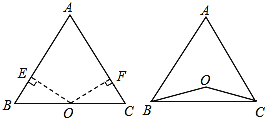
【题目】如图,在正方形ABCD中,G是BC上任意一点,连结AG,DE⊥AG于点E,BF∥DE交AG于点F,探究线段DE,BF,EF三者之间的数量关系,并说明理由.

【答案】DE=BF+EF
【解析】试题分析:DE=BF+EF,根据已知条件易证△ABF≌△DAE,由全等三角形的性质可得BF=AE,AF=DE,根据图中相关线段的和差关系得到DE=BF+EF.
试题解析:
DE=BF+EF.理由如下:
∵四边形ABCD是正方形,
∴AB=DA,∠DAB=∠ABC=90°.
∵DE⊥AG于点E,BF∥DE交AG于点F,
∴∠DEA=∠DEF=∠AFB=90°,
∴∠ADE+∠DAE=90°.
∵∠DAE+∠BAF=90°,
∴∠ADE=∠BAF.
在△ABF和△DAE中,
∵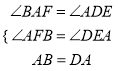
∴△ABF≌△DAE(AAS).
∴BF=AE,AF=DE.
∵AF=AE+EF,
∴DE=BF+EF.

练习册系列答案
相关题目