Question

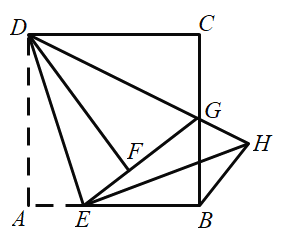
【题目】如图，在正方形ABCD中，E为边AB上一点，沿DE将折叠得到，延长EF交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH.

（1）求证：GF=GC；

（2）探求BH与AE数量关系，并说明理由.

Answer 1

【答案】（1）见解析；（2），理由见解析

【解析】

（1）根据对称得△ADE≌△FDE，再由HL证明Rt△DFG≌Rt△DCG，可得结论；

（2）作如图辅助线，构建全等三角形，证明△ADE≌△PEH，得AD=PE，AE=PH，再说明△BPH是等腰直角三角形，即可得结论．

（1）∵四边形ABCD是正方形，
∴DA=DC，∠A=∠C=90°，
∵沿DE将折叠得到，
∴△ADE≌△FDE，
∴DA=DF=DC，∠DFE=∠A=90°，
∴∠DFG=90°，
在Rt△DFG和Rt△DCG中，

，
∴Rt△DFG≌Rt△DCG（HL），
∴GF=GC；

（2），

理由如下：过点H作HP⊥AB，垂足为P，

由（1）知，∠ADE=∠FDE，∠FDG=∠CDG，

∵∠ADC=90°，

∴∠EDG=45°，

∵EH⊥DE，

∴是等腰直角三角形，

∴DE=EH，

∵∠ADE+∠AED=∠AED+∠PEH=90°，

∴∠ADE=∠PEH，

在△ADE和△PEH中，

，

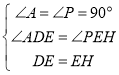∴△ADE≌△PEH，

∴AD=PE，AE=PH，

∴AD=AB=EP，

∴AE=BP=PH，

∴△BPH为等腰直角三角形，

∴．