题目内容
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A, ![]() .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 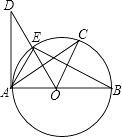
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
【答案】D
【解析】解:∵AB是⊙O的直径,AD切⊙O于点A, ∴BA⊥DA,故A正确;
∵ ![]() ,
,
∴∠EAC=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠EAC=∠ACO,
∴OC∥AE,故B正确;
∵∠COE是 ![]() 所对的圆心角,∠CAE是
所对的圆心角,∠CAE是 ![]() 所对的圆周角,
所对的圆周角,
∴∠COE=2∠CAE,故C正确;
只有当 ![]() =
= ![]() 时OD⊥AC,故本选项错误.
时OD⊥AC,故本选项错误.
故选D.
【考点精析】掌握圆心角、弧、弦的关系和圆周角定理是解答本题的根本,需要知道在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目