Question

【题目】已知半圆O，点C、D在弧AB上，连接AD、BD、CD，∠BDC+2∠ABD＝90°．

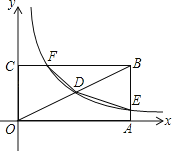
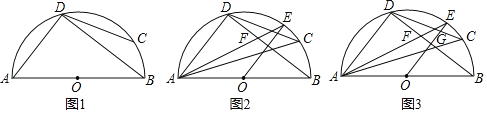
（1）如图1，求证：DA＝DC；

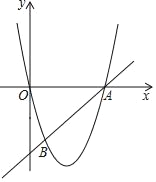
（2）如图2，作OE⊥BD交半圆O于点E，连接AE交BD于点F，连接AC，求证：∠DFA＝∠DAC+∠DAE；

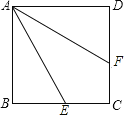
（3）如图3，在（2）的条件下，设AC交BD于点G，FG＝1，AG＝5，求半圆O的半径．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）连接OD，OC，根据同弧所对的圆心角等于圆周角的2倍得到∠BOC+2∠AOD＝180°，再根据∠BOC+∠AOD+∠COD＝180°，即可得到∠AOD＝∠COD，由此得到结论；

（2）根据垂径定理得到∠DAE＝∠EAB，由（1）的结论可得到∠DBA＝∠DAC，再根据三角形外角的性质得到结论；

（3）过点A作AM⊥AB，交BD的延长线于点M，连接OD交AC于N，根据等角对等边求出AM=AG=5，根据AB是直径证得∠MAD＝∠ABD，再由∠DAE＝∠EAB得到∠MAE＝∠MFA，从而求出AM＝MF＝5，根据等腰三角形的三线合一的性质求出DM，根据勾股定理求出AD，再根据三角函数求出AB即可得到半径的长.

证明：（1）如图1，连接OD，OC，

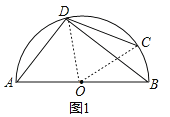
∵∠BOC＝2∠BDC，∠AOD＝2∠ABD，∠BDC+2∠ABD＝90°，

∴∠BOC+2∠AOD＝180°，

∵∠BOC+∠AOD+∠COD＝180°，

∴∠AOD＝∠COD，

∴AD＝CD；

（2）如图2，∵OE⊥BD，

∴,

∴∠DAE＝∠EAB，

∵AD＝CD，

∴∠DAC＝∠C，且∠DBA＝∠C，

∴∠DBA＝∠DAC，

∴∠DFA＝∠EAB+∠DBA＝∠DAE+∠DAC；

（3）如图2，过点A作AM⊥AB，交BD的延长线于点M，连接OD交AC于N，

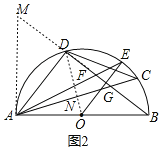
∵OD＝OB，

∴∠ABD＝∠ODB，

∵AD＝CD，

∴OD⊥AC，

∴∠AGD+∠ODB＝90°，

∵∠MAB＝90°，

∴∠ABD+∠M＝90°，

∴∠M＝∠AGD，

∴AM＝AG＝5，

∵AB是直径，

∴∠ADB＝90°，

∴∠M+∠MAD＝90°，

∴∠MAD＝∠ABD，

∴∠MAD+∠DAE＝∠ABD+∠EAB，

∴∠MAE＝∠MFA，

∴AM＝MF＝5，

∴MG＝MF+FG＝6，

∵AD⊥MG，

∴DM＝DG＝3，

∴DF＝DG﹣FG＝2，

∴AD＝＝4，

∵∠ABD＝∠MAD，

∴sin∠ABD＝sin∠MAD，

∴,

∴,

∴AB＝，

∴OA＝，

∴半圆O的半径．