题目内容
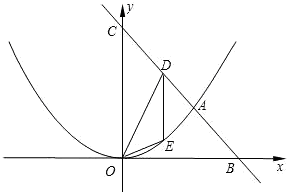
如图,二次函数图象的顶点为坐标系原点O,且经过点A(3,3),一次函数的图象经过点A和点B(6,0).(1)求二次函数与一次函数的解析式;
(2)如果一次函数图象与y轴相交于点C,点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E,∠CDO=∠OED,求点D的坐标;
(3)当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.
分析:(1)利用待定系数分别求出二次函数与一次函数的解析式,二次函数的解析式为y=ax2,一次函数的解析式为y=kx+b;
(2)由DE∥y轴,∠CDO=∠OED,得到△CDO∽△OED,则DO2=DE•CO,设D点的坐标为(m,-m+6),那么点E的坐标为(m,
m2),因此2m2-12m+36=6(-m+6-
m2),解方程得到m=
,即可得到D点坐标;
(3)由OC∥DE,若DE=OC,以点O、C、D、E为顶点的四边形为平行四边形;分类讨论:①当点D在点E上方,-x+6-
x2=6,得x1=0,x2=-3.②当点D在E下方,
x2-(-x+6)=6,得x=
.即可得到D点坐标.
(2)由DE∥y轴,∠CDO=∠OED,得到△CDO∽△OED,则DO2=DE•CO,设D点的坐标为(m,-m+6),那么点E的坐标为(m,
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
(3)由OC∥DE,若DE=OC,以点O、C、D、E为顶点的四边形为平行四边形;分类讨论:①当点D在点E上方,-x+6-
| 1 |
| 3 |
| 1 |
| 3 |
-3±
| ||
| 2 |
解答:解:(1)设二次函数的解析式为y=ax2,把A(3,3)代入得a=
,
∴二次函数的解析式为y=
x2;
设一次函数的解析式为y=kx+b,
把A(3,3),B(6,0)分别代入得,3k+b=3,6k+b=0,解得k=-1,b=6,
∴一次函数的解析式为y=-x+6;
(2)∵DE∥y轴,∠CDO=∠OED,
∴△CDO∽△OED,
∴
=
,即DO2=DE•CO,
设D点的坐标为(m,-m+6),那么点E的坐标为(m,
m2),
∴OD2=m2+(m-6)2=2m2-12m+36,DE=-m+6-
m2,
又∵由直线y=-x+6与y轴交于点C,
∴点C的坐标为(0,6),CO=6,
∴2m2-12m+36=6(-m+6-
m2),
解得m1=0(不合题意,舍去),m2=
,
∴点D的坐标为(
,
);
(3)以点O、C、D、E为顶点的四边形能成为平行四边形.理由如下:
若DE=OC,以点O、C、D、E为顶点的四边形为平行四边形,
①当点D在点E上方,-x+6-
x2=6,得x1=0,x2=-3.x=0(舍去),x=-3,y=-(-3)+3=6
②当点D在E下方,
x2-(-x+6)=6,得x=
.
当x=
,y=-
+6=
;
当x=
,y=-
+6=
.
所以当D点坐标为:(-3,6)或(
,
)或(
,
).
| 1 |
| 3 |
∴二次函数的解析式为y=
| 1 |
| 3 |
设一次函数的解析式为y=kx+b,
把A(3,3),B(6,0)分别代入得,3k+b=3,6k+b=0,解得k=-1,b=6,
∴一次函数的解析式为y=-x+6;
(2)∵DE∥y轴,∠CDO=∠OED,
∴△CDO∽△OED,
∴
| DE |
| DO |
| DO |
| CO |
设D点的坐标为(m,-m+6),那么点E的坐标为(m,
| 1 |
| 3 |
∴OD2=m2+(m-6)2=2m2-12m+36,DE=-m+6-
| 1 |
| 3 |
又∵由直线y=-x+6与y轴交于点C,
∴点C的坐标为(0,6),CO=6,
∴2m2-12m+36=6(-m+6-
| 1 |
| 3 |
解得m1=0(不合题意,舍去),m2=
| 3 |
| 2 |
∴点D的坐标为(
| 3 |
| 2 |
| 9 |
| 2 |
(3)以点O、C、D、E为顶点的四边形能成为平行四边形.理由如下:
若DE=OC,以点O、C、D、E为顶点的四边形为平行四边形,
①当点D在点E上方,-x+6-
| 1 |
| 3 |
②当点D在E下方,
| 1 |
| 3 |
-3±
| ||
| 2 |
当x=
-3+
| ||
| 2 |
-3+
| ||
| 2 |
15-
| ||
| 2 |
当x=
-3-
| ||
| 2 |
-3-
| ||
| 2 |
15+
| ||
| 2 |
所以当D点坐标为:(-3,6)或(
-3+
| ||
| 2 |
15-
| ||
| 2 |
-3-
| ||
| 2 |
15+
| ||
| 2 |
点评:本题考查了用待定系数法求二次函数的解析式.也考查了平行四边形的性质和点在图象上,点的横纵坐标满足图象的解析式以及一元二次方程的解法.

练习册系列答案
相关题目
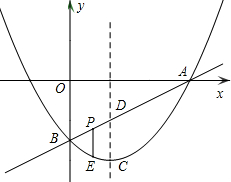 段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.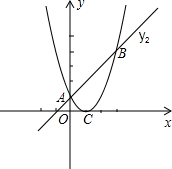 如图,二次函数
如图,二次函数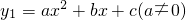 的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.
的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.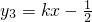 (k>0)与函数f的图象只有两个交点时,求k的值.
(k>0)与函数f的图象只有两个交点时,求k的值.


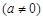 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、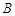 两点(
两点( :
: 对称.
对称.
 在直线
在直线 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 、
、 、
、 ,求
,求 和的最小值.
和的最小值.