题目内容
已知如图,二次函数
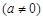 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、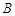 两点(
两点(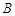 在
在 点右侧),点
点右侧),点 、
、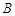 关于直线
关于直线 :
: 对称.
对称.

(1)求 、
、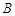 两点坐标,并证明点
两点坐标,并证明点 在直线
在直线 上;
上;
(2)求二次函数解析式;
(3)过点 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、 、
、 ,求
,求 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即 和的最小值
和的最小值
【答案】
解:(1)依题意,得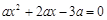
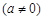
解得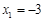 ,
,
∵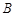 点在
点在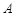 点右侧
点右侧
∴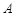 点坐标为
点坐标为 ,
,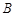 点坐标为
点坐标为 (2分)
(2分)
∵直线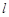 :
:
当 时,
时,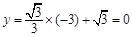

∴点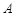 在直线
在直线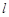 上 (3分)
上 (3分)
(2)∵点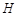 、
、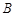 关于过
关于过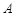 点的直线
点的直线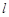 :
: 对称
对称
∴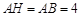
过顶点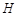 作
作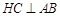 交
交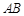 于
于 点则
点则 ,
,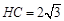
∴顶点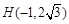 (5分)
(5分)
把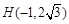 代入二次函数解析式,解得
代入二次函数解析式,解得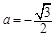
∴二次函数解析式为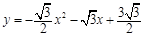 (7分)
(7分)
(3)直线 的解析式为
的解析式为
直线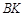 的解析式为
的解析式为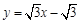
由 解得
解得 即
即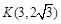 ,则
,则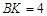
∵点 、
、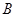 关于直线
关于直线 对称
对称
∴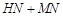 的最小值是
的最小值是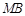 ,
,
过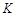 作
作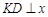 轴于D点。
轴于D点。
过点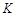 作直线
作直线 的对称点
的对称点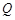 ,连接
,连接 ,交直线
,交直线 于
于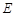
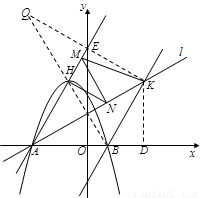
则 ,
, ,
,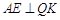
∴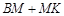 的最小值是
的最小值是 ,即
,即 的长
的长
是 的最小值
的最小值
∵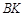 ∥
∥
∴
在Rt△BKQ, 由勾股定理得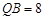 (10分)
(10分)
∴ 的最小值为
的最小值为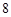 (不同解法参照给分)
(不同解法参照给分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

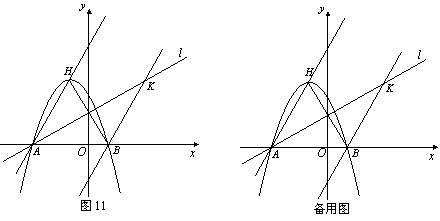


 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、 两点(
两点( :
: 对称.
对称.
 在直线
在直线 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 、
、 、
、 ,求
,求 和的最小值.
和的最小值. 