Question

【题目】在平面直角坐标系中，点A的坐标为．

（1）如图1，若点B 在x轴正半轴上，点，，，求点B坐标；

（2）如图2，若点B 在x轴负半轴上，轴于点E，轴于点F，，MF交直线AE于点M，若点，BM=5，求点M坐标.

Answer 1

【答案】（1）B（4，0）；（2）M（3,-3）

【解析】

（1）作AD⊥x轴，CE⊥x轴，垂足分别为D、E，先利用AAS定理证明△ADB≌△BEC得出BD=CE，从而求出OD，CE，最后进一步求解即可；

（2）在AM上截取AN=OB，连接FN，先后根据SAS定理证明△BOF≌△NAF与△BFM≌△NFM，然后进一步求出NM，AN的值，最后根据题求解即可.

（1）如图1：作AD⊥x轴，CE⊥x轴，垂足分别为D、E，

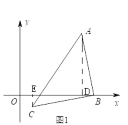
∴∠ADB=∠BEC=90°，

∴∠DAB+∠ABD=90°，

∵AB⊥BC，

∴∠EBC+∠ABD=90°，

∴∠DAB=∠ABC，

在△ADB与△BEC中，

∵∠ADB=∠BEC，∠DAB=∠EBC，AB=BC，

∴△ADB≌△BEC（AAS），

∴BD=CE,

∵A(3,3)，C(-1,1),

∴OD=3,CE=1,

∴OB=OD+BD=OD+CE=3+1=4,

∴B点坐标为(4,0).

（2）如图2：在AM上截取AN=OB，连接FN，

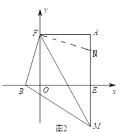
∵A(3,3),

∴OF=AF=OE=3,

在△BOF与△NAF中，

∵AN=OB，∠A=∠BOF，OF=AF，

∴△BOF≌△NAF(SAS),

∴BF=NF，∠BFO=∠NFA，

∵∠BFM=∠BFO+∠OFM=45°，

∴∠NFA+∠OFM=45°，

∴∠OFA=90°，

∴∠NFM=∠OFA-∠NFA-∠OFM=45°，

∴∠BFM=∠NFM，

在△BFM与△NFM中，

∵BF=AN，∠BFM=∠NFM，FM=FM，

∴△BFM≌△NFM(SAS)，

∴BM=NM,

∵BM=5，B(-1,0)，

∴NM=5，OB=AN=1,

∴EM=AN+NM-AE=3,

∴M点坐标为（3，-3）.