题目内容
【题目】如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD,且AD=4,点P为线段AC上一动点,连接BP.则2BP+AP的最小值为__________.

【答案】![]()
【解析】
先证明△ABD是等边三角形可得∠PAF=30°,作PF⊥AD于F,BF′⊥AD于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=![]() PA,推出2BP+AP=2(PB+
PA,推出2BP+AP=2(PB+![]() PA)=2(PB+PF),所以当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,求出BF′即可解决问题.
PA)=2(PB+PF),所以当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,求出BF′即可解决问题.
∵∠ACB=90°,∠BAC=30°
∴AC⊥BD,∠B=60°
∵DC=CB,
∴AD=AB,∵∠B=60°,
∴△ABD是等边三角形,
∴∠PAF=30°,
作PF⊥AD于F,EF′⊥AD于F′,交AC于P′.
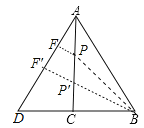
∵∠PAF=30°,∠PFA=90°,
∴PF=![]() PA,
PA,
∴2BP+AP=2(PB+![]() PA)=2(PB+PF),
PA)=2(PB+PF),
∴当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,
在Rt△DF′B中,∵∠D=60°,DB=4,
∴∠DBF′=30°
∴DF′=2,
∴BF′=![]()
∴2BP+AP的最小值为4![]() .
.

练习册系列答案
相关题目







