题目内容
【题目】如图,已知在△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9, 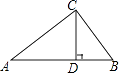
(1)求DC、AB的长;
(2)求证:△ABC是直角三角形.
【答案】
(1)解:∵在Rt△BCD中,BC=15,BD=9,
∴CD= ![]() =
= ![]() =12.
=12.
在Rt△ADC中,AC=20,CD=12,
∴AD= ![]() =
= ![]() =16.
=16.
∴AB=AD+DB=16+9=25
(2)解:∵AB=25,AC=20,BC=15,
∴AB2=252=625,AC2+BC2=202+152=625,
∴AB2=AC2+BC2,
∴△ABC是直角三角形
【解析】(1)在Rt△BCD中利用勾股定理求得CD的长,然后在Rt△ADC中求得AD的长,根据AB=AD+DB即可求解;(2)利用勾股定理的逆定理即可判断.
【考点精析】本题主要考查了勾股定理的概念和勾股定理的逆定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目