题目内容
【题目】Rt△ABC中,∠BAC=90°,AB=AC=2.以AC为一边,在△ABC外部作等腰直角三角形ACD,则线段BD的长为 .
【答案】4或2 ![]() 或
或 ![]()
【解析】解:①以A为直角顶点,向外作等腰直角三角形DAC, 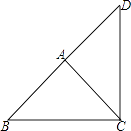
∵∠DAC=90°,且AD=AC,
∴BD=BA+AD=2+2=4;
②以C为直角顶点,向外作等腰直角三角形ACD,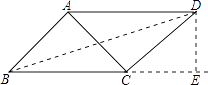
连接BD,过点D作DE⊥BC,交BC的延长线于E.
∵△ABC是等腰直角三角形,∠ACD=90°,
∴∠DCE=45°,
又∵DE⊥CE,
∴∠DEC=90°,
∴∠CDE=45°,
∴CE=DE=2× ![]() =
= ![]() ,
,
在Rt△BAC中,BC= ![]() =2
=2 ![]() ,
,
∴BD= ![]() =
= ![]() =2
=2 ![]() ;
;
③以AC为斜边,向外作等腰直角三角形ADC,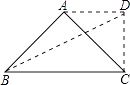
∵∠ADC=90°,AD=DC,且AC=2,
∴AD=DC=ACsin45°=2× ![]() =
= ![]() ,
,
又∵△ABC、△ADC是等腰直角三角形,
∴∠ACB=∠ACD=45°,
∴∠BCD=90°,
又∵在Rt△ABC中,BC= ![]() =2
=2 ![]() ,
,
∴BD= ![]() =
= ![]() =
= ![]() .
.
故BD的长等于4或2 ![]() 或
或 ![]() .
.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目