题目内容
【题目】如图①、②,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段![]() 的端点在格点上.
的端点在格点上.
(1)在图①中找到一个格点,使![]() ∠
∠![]() =
=![]() ,并画出这个三角形.
,并画出这个三角形.
(2)在图②中找到一个格点![]() ,使点
,使点![]() 或
或![]() 为顶点的角的正切值为1,并画出这个三角形.
为顶点的角的正切值为1,并画出这个三角形.
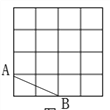

图① 图②
【答案】(1)图形见解析(2)图形见解析
【解析】试题分析:
(1) 由于网格是由全等的正方形组成的,点A和点B均在格点上,所以点A和点B以及点A正右方的第二个格点(设该格点为点O)构成Rt△AOB. 在Rt△AOB中,易知![]() ,故只要将在直线OA上的某个格点(点A除外)选作点C均可使
,故只要将在直线OA上的某个格点(点A除外)选作点C均可使![]() .
.
(2) 要使以点A为顶点的角的正切值为1,可以考虑以点A为一个底角顶点,以B为直角顶点构造等腰直角三角形. 利用正方形的边长和勾股定理可以求得线段AB的长为![]() ,则另一条腰的长度也应为
,则另一条腰的长度也应为![]() . 不难找到与点B的距离为
. 不难找到与点B的距离为![]() 的格点(点A除外). 将点A与点B以及新找到的格点连成三角形,利用勾股定理的逆定理判断该三角形是否为直角三角形. 若此三角形是直角三角形则该格点为所求的点D,该三角形也为所求的三角形. 同理,要使以点B为顶点的角的正切值为1,可以考虑以点B为一个底角顶点,以A为直角顶点构造等腰直角三角形.
的格点(点A除外). 将点A与点B以及新找到的格点连成三角形,利用勾股定理的逆定理判断该三角形是否为直角三角形. 若此三角形是直角三角形则该格点为所求的点D,该三角形也为所求的三角形. 同理,要使以点B为顶点的角的正切值为1,可以考虑以点B为一个底角顶点,以A为直角顶点构造等腰直角三角形.
试题解析:
(注:答案不唯一,以下答案供参考)
(1) 由题意可以画出下列三角形.
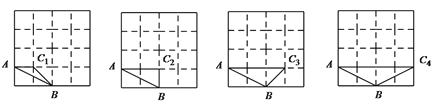
(2) 若点A为顶点的角的正切值为1,则可画出如下三角形.
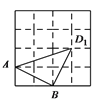
若点B为顶点的角的正切值为1,则可画出如下三角形.
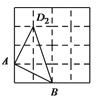

【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
