题目内容
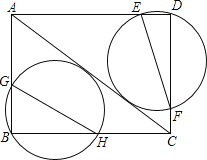
【题目】如图,在矩形ABCD中,BC=8,AB=6,经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是( )
A.6 B.8 C.9.6 D.10
【答案】C
【解析】
试题分析:如图,设GH的中点为O,过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,根据∠B=90°可知,点O为过B点的圆的圆心,OM为⊙O的半径,BO+OM为直径,可知BO+OM≥BN,故当BN为直径时,直径的值最小,即直径GH也最小,同理可得EF的最小值.
解:如图,设GH的中点为O,
过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,
在Rt△ABC中,BC=8,AB=6,
∴AC=![]() =10,
=10,
由面积法可知,BN![]() AC=AB
AC=AB![]() BC,
BC,
解得BN=4.8,
∵∠B=90°,
∴GH为⊙O的直径,点O为过B点的圆的圆心,
∵⊙O与AC相切,
∴OM为⊙O的半径,
∴BO+OM为直径,
又∵BO+OM≥BN,
∴当BN为直径时,直径的值最小,
此时,直径GH=BN=4.8,
同理可得:EF的最小值为4.8,
∴EF+GH的最小值是9.6.
故选C.


练习册系列答案
相关题目