Question

4．一个底面半径为α，高为h的圆柱体木块，削成一个最大的长方体．则削去了原来的$\frac{1}{3}$（π取3）．

Answer 1

分析 削去的体积=圆柱的体积-长方体的体积，根据题干分析可得，削出的这个长方体的高是h，底面积是圆柱的底面圆的内接正方形，这个正方形的面积=圆柱的底面直径×半径，即2a²，由此利用圆柱和长方体的体积公式即可求出削去的体积，最后除以原来圆柱体的体积即可．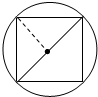

解答 解：3×a²×h-2a×a×h
=3a²h-2a²h
=a²h
a²h÷（3×a²×h）
=a²h÷3a²h
=$\frac{1}{3}$
答：削去了原来的$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．

点评 此题考查圆柱和长方体的体积公式的灵活应用，关键是根据圆内接正方形的特点求出长方体的底面积．