Question

10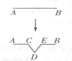．对于一个多边形，定义一种“生长”操作（如图），将其中一边AB变成折线ACDEB，其中C和E是AB的三等分点，C、D、E三点可构成等边三角形，那么，一个边长是9的等边三角形，经过四次“生长”操作得到的图形的周长是85$\frac{1}{3}$．

Answer 1

分析 根据“一边AB变成折线ACDEB，其中C和E是AB的三等分点，C、D、E三点可构成等边三角形”得到CD=DE=CE=AC=EB=$\frac{1}{3}$AB，则AC+CD+DE+EB=$\frac{1}{3}$AB×4，按照次规律，每次“生长”，都变成原来的$\frac{4}{3}$，即为一个以$\frac{4}{3}$为等比的等比数列．

解答 解：边长是9的等边三角形的周长是9×3=27
第一次“生长”，得到的图形的周长是：27×$\frac{4}{3}$=36
第二次“生长”，得到的图形的周长是：36×$\frac{4}{3}$=48
第三次“生长”，得到的图形的周长是：48×$\frac{4}{3}$=64
第四次“生长”，得到的图形的周长是：64×$\frac{4}{3}$=$\frac{256}{3}$=85$\frac{1}{3}$
答：经过四次“生长”操作得到的图形的周长是85$\frac{1}{3}$．
故答案为：85$\frac{1}{3}$．

点评 主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．