Question

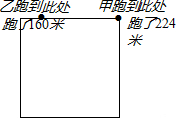
甲、乙分别从一个周长为224米的正方形围墙的对角顶点同时出发绕围墙跑（如图）．甲每秒跑7米，乙每秒跑5米，经过

32

秒钟后，甲第一次看见乙，甲追上乙要用上

56

秒．

Answer 1

分析：（1）首先根据正方形围墙的周长先计算出正方形围墙一面墙的边长为56米，因为甲和乙都从正方形的对角顶点同时出发，只有当甲乙在同一边上时，甲才能看到乙；接着用估计的方法，甲跑3面墙跑了56×3=168米，用了168除以7得24分钟，这时乙跑了24×5=120米，过了2面墙且到了第三面墙的8米处，这时甲还看不到乙，甲再走一面墙到了甲的出发点，又用了56÷7=8分钟，乙就又走了8×5=40米，这时说明乙在从他开始的第三面墙的8+40=48米处，此时甲能看到乙了；
（2）因为甲和乙都从正方形围墙的对角顶点出发，甲和乙相距两个正方形的边长，即56×2═112（米），甲比乙每秒多行7-5=2（米），看112米里面有几个2米即得甲追上乙要用的时间．

解答：解：（1）正方形围墙一面墙的边长：224÷4═56（米），
甲跑完一周用的时间：224÷7=32（秒），
32秒乙跑得路程：32×5=160（米），56×3=168（米），160＜168，
说明乙在从他开始跑得第三面的边中，这时甲正好在这面墙的顶点处，也即经过32秒甲能看到乙了；

（2）甲追上乙要用：（ 56×2）÷（7-5），
=112÷2，
=56（秒）．
 答：经过32秒钟后，甲第一次看到乙，甲追上乙要用56秒．

点评：此题属于追及问题的应用题，解决关键是要理解只有当甲乙在同一边上时，甲才能看到乙，进而得出答案．