题目内容
有一串分数排列如下: 、
、 、
、 、
、 、
、 、
、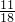 …,那么这列数的第100个数是
…,那么这列数的第100个数是
- A.

- B.

- C.

- D.

A
分析: =
=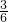 ;
; =
=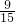 ,这个数列就是:
,这个数列就是:
 、
、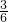 、
、 、
、 、
、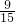 、
、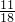 …,
…,
分子:1、3、5、7、9、11…后一个比前一个大2,可以看成公差是2的等差数列,由此求出第100个数的分子;
分母:3,6,9,12,15,18,…后一个比前一个大3,看成公差是3的等差数列,由此求出第100个数的分母;进而求出第100个数是几.
解答:第100个数的分子是:
1+(100-1)×2,
=1+99×2,
=1+198,
=199;
分母是:
3+(100-1)×3,
=3+99×3,
=3×(1+99),
=3×100,
=300;
这个分数就是 .
.
故选:A.
点评:本题关键是能通过给出的分数分别找出分子和分母的变化规律,然后根据等差数列的通项公式:第n项=首项+(n-1)×公差求解.
分析:
 =
=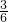 ;
; =
=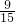 ,这个数列就是:
,这个数列就是: 、
、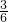 、
、 、
、 、
、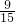 、
、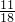 …,
…,分子:1、3、5、7、9、11…后一个比前一个大2,可以看成公差是2的等差数列,由此求出第100个数的分子;
分母:3,6,9,12,15,18,…后一个比前一个大3,看成公差是3的等差数列,由此求出第100个数的分母;进而求出第100个数是几.
解答:第100个数的分子是:
1+(100-1)×2,
=1+99×2,
=1+198,
=199;
分母是:
3+(100-1)×3,
=3+99×3,
=3×(1+99),
=3×100,
=300;
这个分数就是
 .
.故选:A.
点评:本题关键是能通过给出的分数分别找出分子和分母的变化规律,然后根据等差数列的通项公式:第n项=首项+(n-1)×公差求解.

练习册系列答案
相关题目