题目内容
已知阴影部分的面积是50平方厘米，求三角形ABC的面积．
分析：如图所示：
，AB的中点为D，AC的中点为E，所以DE是三角形ABC的中位线，BC=2DE，那么三角形ABC的高=三角形BDE的高×2，所以三角形ABC的面积=三角形ADE的面积×2×2．据此解答即可．
，AB的中点为D，AC的中点为E，所以DE是三角形ABC的中位线，BC=2DE，那么三角形ABC的高=三角形BDE的高×2，所以三角形ABC的面积=三角形ADE的面积×2×2．据此解答即可．解答：解：如图所示：，
AB的中点为D，AC的中点为E，BC=2DE，三角形ABC的高=三角形BDE的高×2，
所以三角形ABC的面积为：
50×2×2
=100×2
=200（平方厘米）．
答：三角形ABC的面积是200平方厘米．
，AB的中点为D，AC的中点为E，BC=2DE，三角形ABC的高=三角形BDE的高×2，
所以三角形ABC的面积为：
50×2×2
=100×2
=200（平方厘米）．
答：三角形ABC的面积是200平方厘米．
点评：解决本题关键是根据一个三角形的底和高分别是另一个三角形的底和高的2倍，那么面积就是它的4倍．
练习册系列答案
相关题目
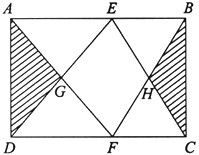如图，在长方形ABCD中，AE=DF，已知阴影部分的面积是16cm2，四边形EGFH的面积是
如图，E、F分别是梯形ABCD两腰上的中点，已知阴影部分的面积是43c㎡，那么梯形ABCD的面积是
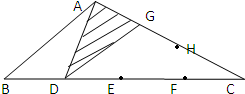在三角形ABC中，如图：BD=DE=EF=FC，AG=GH=HC．已知阴影部分的面积是20平方厘米，那么三角形ABC的面积是
在如图的梯形中，已知阴影部分的面积是15平方厘米，那么这个梯形的面积是