题目内容
（2012?北京模拟）有两种不同形状的纸板，一种是正方形的，另一种是长方形的，正方形纸板的总数与长方形纸板的总数之比是1：2．用这些纸板做成一些竖式和横式的无盖纸盒．正好将纸板用完．问在所做的纸盒中，竖式纸盒的总数与横式纸盒的总数之比是多少？
分析：竖式纸盒要用1个正方形纸板和4个长方形纸板，横式纸盒要用2个正方形纸板和3个长方形纸板，设竖式纸盒有x个，横式纸盒有y个，根据题意即可解决问题．．
解答：解：设竖式纸盒有x个，横式纸盒有y个，那么
正方形纸板一共有（x+2y）个，长方形纸板一共有（4x+3y）个，根据题意可得：
（x+2y）：（4x+3y）=1：2
根据比例的基本性质和等式的性质解得：
x：y=1：2
答：坚式纸盒的总数与横式纸盒的总数之比是 1：2．
故答案为：1：2．．
正方形纸板一共有（x+2y）个，长方形纸板一共有（4x+3y）个，根据题意可得：
（x+2y）：（4x+3y）=1：2
根据比例的基本性质和等式的性质解得：
x：y=1：2
答：坚式纸盒的总数与横式纸盒的总数之比是 1：2．
故答案为：1：2．．
点评：此题考查的是比的意义，应结合题意，认真分析，解答即可．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
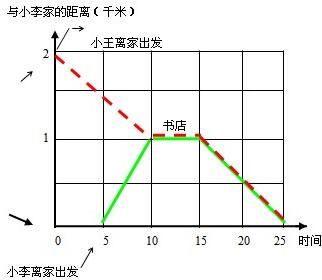（2012?北京模拟）下面是小王和小李外出情况的一张折线统计图．他们分别住在一条大街的两头，相距2千米，在他们两家之间，中途恰好是一所书店．现在请根据下图，回答问题：