题目内容
 下列竖式中的A、B、C、D、E分别代表1~9中不同的数字,求出它们使竖式成立的值.则:ABCDE=
下列竖式中的A、B、C、D、E分别代表1~9中不同的数字,求出它们使竖式成立的值.则:ABCDE=42857
42857
.分析:根据题意,由整数乘法竖式计算的方法进行解答即可.
解答:解:根据题意可得:
个位上:E×3的末尾是1,因为,7×3=21,所以可得:E=7,向十位上进2;
十位上:D×3+2的末尾是E,即是7,因为,5×3+2=17,所以可得:D=5,向百位上进1;
百位上:C×3+1的末尾是D,即是5,因为,8×3+1=25,所以可得:C=8,向千位上进2;
千位上:B×3+2的末尾是C,即是8,因为,2×3+2=8,所以可得:B=2;
万位上:A×3的末尾是B,即是2,因为,4×3=12,所以可得:A=4,向十万位上进1;
十万位上:1×3+1=4,正好等于A;
由以上推算可得竖式是:
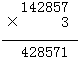
所以,ABCDE=42857.
故答案为:42857.
个位上:E×3的末尾是1,因为,7×3=21,所以可得:E=7,向十位上进2;
十位上:D×3+2的末尾是E,即是7,因为,5×3+2=17,所以可得:D=5,向百位上进1;
百位上:C×3+1的末尾是D,即是5,因为,8×3+1=25,所以可得:C=8,向千位上进2;
千位上:B×3+2的末尾是C,即是8,因为,2×3+2=8,所以可得:B=2;
万位上:A×3的末尾是B,即是2,因为,4×3=12,所以可得:A=4,向十万位上进1;
十万位上:1×3+1=4,正好等于A;
由以上推算可得竖式是:
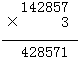
所以,ABCDE=42857.
故答案为:42857.
点评:本题主要考查整数乘法竖式的计算,再根据进位与末尾的数进一步解答即可.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
下列竖式中的字母
a、b、c、s、t各代表什么数字?
|
a =( ); |
b =( ); |
c =( ); |
s =( ); |
t =( ) |




