题目内容
解下列方程
8.2-x=5.5;
5.5+x=7.05;
9x=11.52;
3.78÷x=2.7.
8.2-x=5.5;
5.5+x=7.05;
9x=11.52;
3.78÷x=2.7.
分析:(1)方程的两边同时加上x,再同时减去5.5,即可得解;
(2)方程的两边同时减去5.5,即可得解;
(3)方程的两边同时除以9,即可得解;
(4)方程的两边同时乘x,再同时除以2.7,即可得解.
(2)方程的两边同时减去5.5,即可得解;
(3)方程的两边同时除以9,即可得解;
(4)方程的两边同时乘x,再同时除以2.7,即可得解.
解答:解:(1)8.2-x=5.5
8.2-x+x=5.5+x
8.2=5.5+x
5.5+x-5.5=8.2-5.5
x=2.7;
(2)5.5+x=7.05
5.5+x-5.5=7.05-5.5
x=1.55;
(3)9x=11.52
9x÷9=11.52÷9
x=1.28;
(4)3.78÷x=2.7
3.78÷x×x=2.7×x
2.7x=3.78
2.7x÷2.7=3.78÷2.7
x=1.4.
8.2-x+x=5.5+x
8.2=5.5+x
5.5+x-5.5=8.2-5.5
x=2.7;
(2)5.5+x=7.05
5.5+x-5.5=7.05-5.5
x=1.55;
(3)9x=11.52
9x÷9=11.52÷9
x=1.28;
(4)3.78÷x=2.7
3.78÷x×x=2.7×x
2.7x=3.78
2.7x÷2.7=3.78÷2.7
x=1.4.
点评:在解方程时应根据等式的性质,即等式两边同加上、同减去、同乘上或同除以某一个数(0除外),等式的两边仍相等,同时注意“=”上下要对齐.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
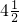 =8.7
=8.7