Question

图ABCD是平行四边形，M是DC的中点，E和F分别位于AB和AD上，且EF平行于BD．若三角形MDF的面积等于5平方厘米，则三角形CEB的面积等于（　　）平方厘米．

A．5

B．10

C．15

D．20

Answer 1

分析：连接FC，DE，FB，在梯形FBCD中，有S△FDB和S△FDC等底等高，所以面积相等；在梯形EBCD中，有S△EDB和S△EBC等底等高，所以面积相等；在梯形FEBD中，有S△FDB和S△EDB等底等高，所以面积相等；所以可得S△FDC=S△EBC，又因为M是DC的中点，根据高一定时，三角形的面积与底成正比例的性质，所以S△EBC=2×5=10cm²．

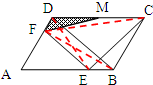
解答：解：如图，连接FC，DE，FB，
在梯形FBCD中，有S△FDB=S△FDC，
在梯形EBCD中，有S△EDB=S△EBC，
在梯形FEBD中，有S△FDB=S△EDB，
所以S△FDC=S△EBC，
因为M是DC的中点，
所以S△EBC=2×5=10（平方厘米）．
则S△EBC=10平方厘米，
答：三角形EBC的面积是10平方厘米．
故选：B．

点评：此题考查了高一定时，三角形的面积与底成正比的关系的灵活应用，正确连接辅助线是解决本题的关键．